
题目列表(包括答案和解析)
14.
13.
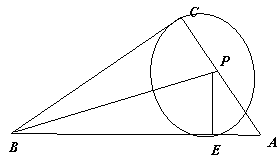
12. (2011湖北宜昌,23,10分)如图1,Rt△ABC两直角边的边长为AC = 1,BC =2.
(1) 如图2, ⊙O 与Rt△ABC的边AB 相切于点X,与边CB相切于点Y.请你在图2 中作出并标明⊙O 的圆心0;(用尺规作图,保留作图痕迹,不写作法和证明)
(2) P 是这个Rt△ABC上和其内部的动点,以P 为圆心的⊙P 与Rt△ABC 的两条边相切.设⊙P 的面积为S,你认为能否确定S 的最大值? 若能,请你求出S 的最大值;若不能,请你说明不能确定S的最大值的理由.
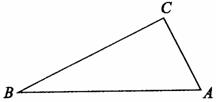

(第23题图1) (第23题图2)
[答案]解:(1)共2分.(标出了圆心,没有作图痕迹的评1分)看见垂足为Y(X)的一 条 垂 线 (或 者∠ABC的平分线)即评1分,
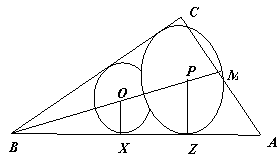
(2)①当⊙P与Rt△ABC的边 AB和BC相切时,由角平分线的性质,动点P是∠ABC的平分线BM上的点,如图1,在∠ABC的平分线BM上任意确定点P1 (不为∠ABC的顶点),∵ OX =BOsin∠ABM,P1Z=BP1sin∠ABM.当 BP1>BO 时 ,P1Z>OX,即P与B的距离越大,⊙P的面积越大.这时,BM与AC的交点P是符合题意的BP长度最大的点.
(3分.此处没有证明和结论不影响后续评分)如图2,∵∠BPA>90°,过点P作PE⊥AB,垂足为E,则E在边AB上.∴以P为圆心、PC为半径作圆,则⊙P与边CB相切于C,与边AB相切于E,即这时的⊙P是符合题意的圆.(4分.此处没有证明和结论不影响后续评分)这时⊙P的面积就是S的最大值.∵∠A=∠A,∠BCA=∠AEP=90°,∴ Rt△ABC∽Rt△APE,(5分)∴ =
= .∵AC=1,BC=2,∴AB=
.∵AC=1,BC=2,∴AB=  .设PC=x,则PA=AC-PC=1-x,PC=PE,
.设PC=x,则PA=AC-PC=1-x,PC=PE,
∴ =
= ,∴x=
,∴x=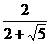 .(6分)
② 如图3,同理可得:当⊙P与Rt△ABC的边AB和AC相切时,
.(6分)
② 如图3,同理可得:当⊙P与Rt△ABC的边AB和AC相切时,
设PC=y,则 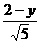 =
= ,∴y=
,∴y=  (7分)
③ 如图4,同理可得:当⊙P与Rt△ABC的边BC和AC相切时,设PF=z,则
(7分)
③ 如图4,同理可得:当⊙P与Rt△ABC的边BC和AC相切时,设PF=z,则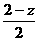 =
= ,∴z=
,∴z=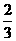 (8分)由①,②,③可知:∵
(8分)由①,②,③可知:∵  >2,∴
>2,∴  +2>
+2> +1>3,∵当分子、分母都为正数时,若分子相同,则分母越小,这个分数越大,(或者:∵x=
+1>3,∵当分子、分母都为正数时,若分子相同,则分母越小,这个分数越大,(或者:∵x=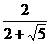 =2
=2 -4, y=
-4, y=  =
= 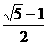 ,
,
∴y-x= >0,∴y>x.
>0,∴y>x.
∵z-y=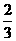 -
- 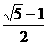 =
=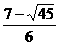 >0,∴2
>0,∴2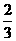 >
>  >
> 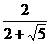 ,(9分,没有过程直接得出酌情扣1分)∴ z>y>x.
,(9分,没有过程直接得出酌情扣1分)∴ z>y>x.
∴⊙P的面积S的最大值为 π.(10分)
π.(10分)

 (第23题答图1)
(第23题答图1)
(第23题答图1)
(第23题答图1)
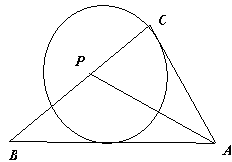
(第23题答图3) (第23题答图4)
11. (2011重庆市潼南,19,6分)画△ABC,使其两边为已知线段a、b,夹角为 .
.
(要求:用尺规作图,写出已知、求作;保留作图痕迹;不在已知的线、角上作图;不
写作法).
 已知:
已知:
求作:
[答案]已知:线段a、b 、角 -------------1分
-------------1分
 求作:△ABC使边BC=a,AC= b,∠C=
求作:△ABC使边BC=a,AC= b,∠C= ------------2分
------------2分
画图(保留作图痕迹图略) --------------6分
10.(2011江苏无锡,26,6分)(本题满分6分)如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°。正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合。现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动。
(1)请在所给的图中,用尺规画出点A在正方形整个翻滚过程中所经过的路线图;
(2)求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ
所围成图形的面积S。


[答案]解:(1)如右图所示.……………………(3分)
(2)S = 2[π·12 + π·()2 + 1 + π·12]
= + 2.………………………(6分)


9. (2011江苏南京,27,9分)如图①,P为△ABC内一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.
⑴如图②,已知Rt△ABC中,∠ACB=90°,∠ACB>∠A,CD是AB上的中线,过点B作BE⊥CD,垂足为E,试说明E是△ABC的自相似点.
⑵在△ABC中,∠A<∠B<∠C.
①如图③,利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹);
②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.


[答案]解:⑴在Rt
△ABC中,∠ ACB=90°,CD是AB上的中线,∴ ,∴CD=BD.
,∴CD=BD.
∴∠BCE=∠ABC.∵BE⊥CD,∴∠BEC=90°,∴∠BEC=∠ACB.∴△BCE∽△ABC.
∴E是△ABC的自相似点.
⑵①作图略.
作法如下:(i)在∠ABC内,作∠CBD=∠A;
(ii)在∠ACB内,作∠BCE=∠ABC;BD交CE于点P.
则P为△ABC的自相似点.
②连接PB、PC.∵P为△ABC的内心,∴ ,
, .
.
∵P为△ABC的自相似点,∴△BCP∽△ABC.
∴∠PBC=∠A,∠BCP=∠ABC=2∠PBC =2∠A,
∠ACB=2∠BCP=4∠A.∵∠A+∠ABC+∠ACB=180°.
∴∠A+2∠A+4∠A=180°.
∴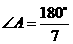 .∴该三角形三个内角的度数分别为
.∴该三角形三个内角的度数分别为 、
、 、
、 .
.
8. (2011重庆綦江,19,6分)为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇所属A村、B村、C村的村委会所在地的距离都相等(A、B、C不在同一直线上,地理位置如下图),请你用尺规作图的方法确定点P的位置.
要求: 写出已知、求作;不写作法,保留作图痕迹.
 解:已知:
解:已知:
求作:
[答案]:解:已知:A、B、C三点不在同一直线上.
求作:一点P,使PA=PB=PC.
(或经过A、B、C三点的外接圆圆心P)
正确作出任意两条线段的垂直平分线,并标出交点P

7. ( 2011重庆江津, 23,10分)A、B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3).
(1)一辆汽车由西向行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离相等,如果有?请用尺规作图找出该点,保留作图痕迹,不求该点坐标.
(2)若在公路边建一游乐场P,使游乐场到两校距离之各最小,通过作图在图中找出建游乐场的位置,并求出它的坐标.

[答案](1)存在满足条件的点C: 作出图形,如图所示,作图略;
(2)作出点A关于x轴的对称点A/(2,-2), 连接A/B,与x轴的交点即为所求的点P.
设A/B所在的直线的解析式为: y=kx+b, 把A/(2,-2), B(7,3)分别代入得:
 解得:
解得: ·
·
所以: y=x-4·
当y=0时,x=4,所以交点P为(4,0)·
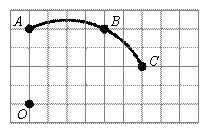
6. (2011甘肃兰州,25,9分)如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C。
(1)请完成如下操作:
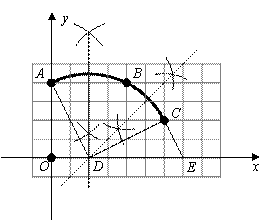
①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长,建立平面直角坐标系;②用直尺和圆规画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连结AD、CD。
(2)请在(1)的基础上,完成下列问题:
①写出点的坐标:C 、D ;
②⊙D的半径= (结果保留根号);
③若扇形ADC是一个圆锥的侧面展开图,则该圆锥的底面面积为 (结果保留π);
④若E(7,0),试判断直线EC与⊙D的位置关系并说明你的理由。

[答案](1)

(2)
① C(6,2),D(2,0)
②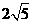
③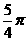
④相切。
理由:∵CD=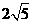 ,CE=
,CE=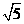 ,DE=5
,DE=5
∴CD2+CE2=25=DE2
∴∠DCE=90°即CE⊥CD
∴CE与⊙D相切。
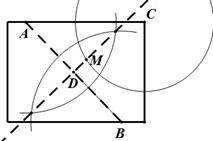
5. (2011四川重庆,20,6分)为进一步打造“宜居重庆”,某区拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请在答题卷的原图上利用尺规作出音乐喷泉M、位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)

[答案]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com