
题目列表(包括答案和解析)
15. (2011湖北襄阳,23,7分)
如图7,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧上一点,连接BD,AD,OC,∠ ADB=30°.
(1)求∠AOC的度数;
(2)若弦BC=6cm,求图中阴影部分的面积.


[答案](1)∵弦BC垂直于半径OA,
∴BE=CE, =·············································································· 1分
又∵∠ADB=30°,∴∠AOC=60°.············································· 2分
(2)∵BC=6,∴ .
.
在Rt△OCE中, .·················································· 3分
.·················································· 3分
∴ ··················································· 4分
··················································· 4分
连接OB. ∵ =
∴∠BOC=2∠AOC=120°··································································· 5分
∴S阴影=S扇形OBC-S△OBC
= =
=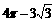 6分
6分
14. (2011贵州贵阳,22,10分)
在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.
(1)圆心O到CD的距离是______;(4分)
(2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)(6分)

(第22题图)
[答案]解:(1)连接OE.
∵CD切⊙O于点E,
∴OE⊥CD.
则OE的长度就是圆心O到CD的距离.
∵AB是⊙O的直径,OE是⊙O的半径,
∴OE=AB=5.
即圆心⊙到CD的距离是5.

(2)过点A作AF⊥CD,垂足为F.
∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,AB∥CD.
∵AB∥CD,OE⊥CD,AF⊥CD,
∴OA=OE=AF=EF=5.
在Rt△ADF中,∠D=60°,AF=5,
∴DF=,
∴DE=5+.
在直角梯形AOED中,OE=5,OA=5,DE=5+,
∴S梯形AOED=×(5+5+)×5=25+.
∵∠AOE=90°,
∴S扇形OAE=×π×52=π.
∴S阴影= S梯形AOED- S扇形OAE=25+-π.
即由弧AE、线段AD、DE所围成的阴影部分的面积为25+-π.
13. (2011山东临沂,23,9分)如图,以O为圆心的圆与△AOB的边AB相切于点C,与OB相交于点D,且OD=BD.已知sinA=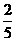 ,AC=
,AC= .
.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
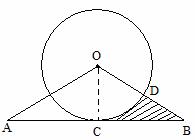
[解](1)连接OC,设OC=r,
∵AC与⊙O相切,
∴OC⊥AC.………………………………………………………………………(1分)
∵sinA=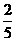 =
= ,
,
∴OA= r,………………………………………………………………………(2分)
r,………………………………………………………………………(2分)
∴AC2=OA2-OC2
=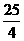 r2-r2=21,……………………………………………………………………( 3分)
r2-r2=21,……………………………………………………………………( 3分)
∴r=2,即⊙O的半径为2.………………………………………………………( 4分)
(2)连接CD,
∵OD=BD,OC⊥BC,
∴CD=OD=OC,………………………………………………………………( 5分)
∴∠COD=60°,………………………………………………………………(6分)
∴BC= OC=2
OC=2 ,………………………………………………………(7分)
,………………………………………………………(7分)
∴S阴影=S△OCB-S扇形OCD
=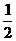 ×2×2
×2×2 -
- π·22
π·22
=2 -
-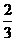 π.………………………………………………………………(9分)
π.………………………………………………………………(9分)
11. (2011广东省,14,6分)如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿着x轴向右平稳4个长度单位得⊙P1.
(1)画出⊙P1,并直接判断⊙P与⊙P1的位置关系;
(2)设⊙P1与x轴正半轴,y轴正半轴的交点为A,B,求劣弧 与弦AB围成的图形的面积(结果保留
与弦AB围成的图形的面积(结果保留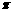 )
)
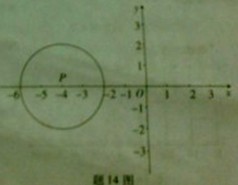
[答案](1)如图所示,两圆外切;

(2)劣弧的长度
劣弧和弦围成的图形的面积为
10.(2011湖南怀化,23,10分) 如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1) 求证:OF∥BC;
(2) 求证:△AFO≌△CEB;
(3) 若EB=5cm,CD=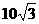 cm,设OE=x,求x值及阴影部分的面积.
cm,设OE=x,求x值及阴影部分的面积.
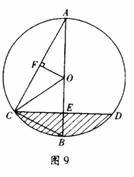
[答案]
解:(1)∵AB为⊙O的直径
∴∠ACB=90°
又∵OF⊥AC于F,∴∠AFO=90°,
∴∠ACB=∠AFO
∴OF∥BC
(2)由(1)知,∠CAB+∠ABC=90°
由已知AB⊥CD于E可得 ∠BEC=90°,∠CBE+∠ABC=90°
∴∠CBE=∠CAB
又∠AFO=∠BEC,BE=OF
∴△AFO≌△CEB
(3)∵AB为⊙O的直径,CD是弦,AB⊥CD于E
∴∠OEC=90°,CE=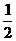 CD=
CD=
在Rt△OCE中,设OE=x,OB=5+x=OC
由勾股定理得:OC2=OE2+EC2
∴(5+x)2=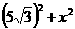 解得x=5.
解得x=5.
在Rt△OCE中
tan∠COE=
∵∠COE为锐角
∴∠OEC=60°
由圆的轴对称性可知阴影部分的面积为:
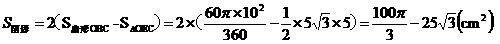
9. (2011福建福州,15,4分)以数轴上的原点 为圆心,
为圆心, 为半径的扇形中,圆心角
为半径的扇形中,圆心角 ,另一个扇形是以点
,另一个扇形是以点 为圆心,
为圆心,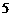 为半径,圆心角
为半径,圆心角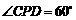 ,点
,点 在数轴上表示实数
在数轴上表示实数 ,如图5.如果两个扇形的圆弧部分(
,如图5.如果两个扇形的圆弧部分( 和
和 )相交,那么实数
)相交,那么实数 的取值范围是
的取值范围是
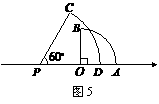

[答案]. 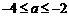
8. (2011福建福州,20,12分)如图9,在 中,
中, ,
, 是
是 边上一点,以
边上一点,以 为圆心的半圆分别与
为圆心的半圆分别与 、
、 边相切于
边相切于 、
、 两点,连接
两点,连接 .已知
.已知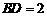 ,
,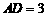 .
.
求:(1) ;
;
(2)图中两部分阴影面积的和.


[答案]解:(1)连接
∵ 、
、 分别切
分别切 于
于 、
、 两点
两点
∴
又∵
∴四边形 是矩形
是矩形
∵
∴四边形 是正方形
是正方形
∴ ∥
∥ ,
,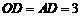
∴
∴在 中,
中,
∴
(2)如图,设⊙O与 交于
交于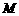 、
、 两点.由(1)得,四边形
两点.由(1)得,四边形 是正方形
是正方形


∴
∴
∵在 中,
中, ,
,
∴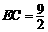
∴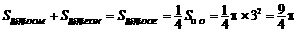
∴
∴图中两部分阴影面积的和为
7. (2011江苏连云港,26,12分)
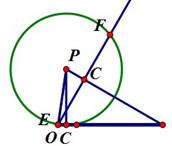
已知∠AOB=60º,半径为3cm的⊙P沿边OA从右向左平行移动,与边OA相切的切点记为点C.
(1)⊙P移动到与边OB相切时(如图),切点为D,求劣弧 的长;
的长;
(2)⊙P移动到与边OB相交于点E,F,若EF= cm,求OC的长.
cm,求OC的长.

第26题
[答案]如图连结PD,PC,且PD⊥OB,PC⊥OA,∵∠AOB=60º,∴∠DPC=120º,由弧长公式可知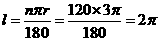 .
.

(2)

6. (2011湖南邵阳,23,8分)数学课堂上,徐老师出示了一道试题:
如图(十)所示,在正三角形ABC中,M是BC边(不含端点B,C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点,若∠AMN=60°,求证:AM=MN。
(1)经过思考,小明展示了一种正确的证明过程,请你将证明过程补充完整。
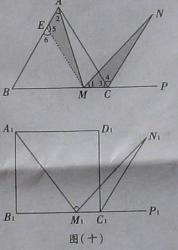 证明:在AB上截取EA=MC,连结EM,得△AEM。
证明:在AB上截取EA=MC,连结EM,得△AEM。
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB -∠B,∠AMN=∠B=60°,
∴∠1=∠2.
又∵CN、平分∠ACP,∴∠4= ∠ACP=60°。
∠ACP=60°。
∴∠MCN=∠3+∠4=120°。………………①
又∵BA=BC,EA=MC,∴BA-EA=BC-MC,即BE=BM。
∴△BEM为等边三角形,∴∠6=60°。
∴∠5=10°-∠6=120°。………………②
由①②得∠MCN=∠5.
在△AEM和△MCN中,
∵__________,____________,___________,
∴△AEM≌△MCN(ASA)。
∴AM=MN.
(2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”(如图),N1是∠D1C1P1的平分线上一点,则当∠A1M1N1=90°时,结论A1M1=M1N1是否还成立?(直接给出答案,不需要证明)
(3)若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”,请你猜想:当∠AnMnNn=______°时,结论AnMn=MnNn仍然成立?(直接写出答案,不需要证明)
[答案]解:(1)∠5=∠MCN,AE=MC,∠2=∠1;
(2)结论成立;
(3) 。
。
5. (2011福建泉州,23,9分)如图,在 中,
中, ,
, 是
是 边
边
 上一点,以
上一点,以 为圆心的半圆分别与
为圆心的半圆分别与 、
、 边相切于
边相切于 、
、 两点,连接
两点,连接 .已知
.已知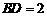 ,
,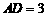 .求:
.求:
(1) ;
;
(2)图中两部分阴影面积的和.
[答案]解:(1)连接
∵ 、
、 分别切
分别切 于
于 、
、 两点
两点
∴
又∵
∴四边形 是矩形
是矩形
∵
∴四边形 是正方形. .................................(2分)
是正方形. .................................(2分)
∴ ∥
∥ ,
,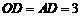
∴
∴在 中,
中,
∴ . .................................(5分)
. .................................(5分)
(2)如图,设 与
与 交于
交于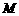 、
、 两点.由(1)得,四边形
两点.由(1)得,四边形 是正方形
是正方形
∴
 ∴
∴
∵在 中,
中, ,
,
∴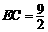 . .................................(7分)
. .................................(7分)
∴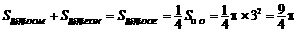
∴
∴图中两部分阴影面积的和为 ............ 9分
............ 9分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com