
题目列表(包括答案和解析)
5. 已知
已知 、
、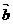 是两个不共线的向量,若它们起点相同,
是两个不共线的向量,若它们起点相同, 、
、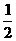
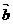 、t(
、t( +
+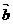 )三向量的终点在一直线上,则实数t=_________.
)三向量的终点在一直线上,则实数t=_________.
[解析]如图, ∵ 、
、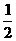
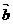 、t(
、t( +
+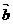 )三向量的终点在一直线上,
)三向量的终点在一直线上,
∴存在实数 使:t(
使:t( +
+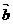 )-
)-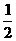
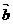 =
= (
( -
-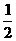
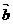 )
)
得(t- )
) =(
=(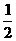 -
-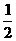
 -t)
-t)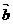
又∵ 、
、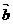 不共线,∴t-
不共线,∴t- =0且
=0且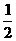 -
-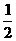
 -t=0
-t=0
解得t=
2、这是一个重要结论,要牢记。
题型2: 用向量法解决几何问题
[例6] 已知
 ABCD的两条对角线AC与BD交于E,O是任意一点,
ABCD的两条对角线AC与BD交于E,O是任意一点,
 求证:
求证: +
+ +
+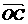 +
+ =4
=4
[解题思路]:由平行四边形的对角线互相平分和相等向 量的定义可得。
量的定义可得。
解析:证明:∵E是对角线AC和BD的交点
∴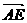 =
=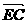 =-
=- ,
, =
=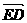 =-
=-
在△OAE中, +
+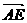 =
=
同理  +
+ =
= ,
, 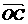 +
+ =
= ,
, +
+ =
=
以上各式相加,得  +
+ +
+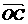 +
+ =4
=4
[名师指引]用向量法解平面几何问题,实质上是将平面几何问题的代数化处理,在解题中应注意进行向量语言与图形语言的互译
[新题导练]
1、逆向应用向量加法运算法则,使得本题的这种证法比其他证法更简便,值得一提的是,一个向量拆成两个向量的和,一定要强化目标意识.
4.如图,在ΔABC中,D、E为边AB的两个三等分点,=3a,=2b,求,.
 解析: =+ = -3a+2b,
解析: =+ = -3a+2b,
因D、E为的两个三等分点,
故= =-a+
=-a+ b =,
b =,
=+=3a-a+ b =2a+
b =2a+ b,
b,
=+=2a+ b-a+
b-a+ b=a+
b=a+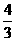 b.
b.
考点三: 向量数乘运算及其几何意义
题型1: 三点共线问题
[例4] 设 是不共线的向量,已知向量
是不共线的向量,已知向量 ,若A,B,D三点共线,求k的值
,若A,B,D三点共线,求k的值
[解题思路]:证明存在实数 ,使得
,使得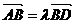
解析: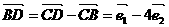 , 使
, 使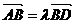

得
[例5] 已知A、B、C、P为平面内四点,求证:A、B、C三点在一条直线上的充要条件是存在一对实数m、n,使=m+n,且m+n=1.
[解题思路]: A、B、C 三点共线的一个充要条件是存在 实数λ,使得=λ.很显然,题设条件中向量表达式并未涉及、,对此,我们不妨利用 =+ 来转化,以便进一步分析求证.
解析:证明 充分性,由=m+n, m+n=1, 得
+=m+n(+)
=(m+n)+n=+n,
∴=n.
∴A、B、C三点共线.
必要性:由A、B、C 三点共线知,存在常数λ,使得=λ,
即 +=λ(+).
=(λ-1)+λ=(1-λ)+λ,
m=1-λ,n=λ,m+n=1,
=m+n.
[名师指引]
3.若3m+2n=a,m-3n=b,其中a,b是已知向量,求m,n.
解析:记3m+2n=a① m-3n=b②
3×②得3m-9n=3b③
①-③得11n=a-3b. ∴n= a-
a- b④
b④
将④代入②有:m=b+3n= a+
a+ b
b
2.下列命题正确的是( )
A.a与b共线,b与c共线,则a与c也共线
B.任意两个相等的非零向量的始点与终点是一平行四边形的四顶点
C.向量a与b不共线,则a与b都是非零向量
D.有相同起点的两个非零向量不平行
解:由于零向量与任一向量都共线,所以A不正确;由于数学中研究的向量是自由向量,所以两个相等的非零向量可以在同一直线上,而此时就构不成四边形,根本不可能是一个平行四边形的四个顶点,所以B不正确;向量的平行只要方向相同或相反即可,与起点是否相同无关,所以D不正确;对于C,其条件以否定形式给出,所以可从其逆否命题来入手考虑,假若a与b不都是非零向量,即a与b至少有一个是零向量,而由零向量与任一向量都共线,可有a与b共线,不符合已知条件,所以有a与b都是非零向量,所以应选C.
考点二: 向量的加、减法
题型1: 考查加加、减法运算及相关运算律
[例2] 化简
[解题思路]:考查向量的加、减法,及相关运算律。
解法一(统一成加法)
 =
=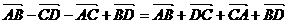
=
解法二(利用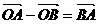 )
)
 =
=
=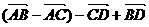
=
解法三(利用 )
)
设O是平面内任意一点,则 =
=
=
=
[名师指引]掌握向量加减的定义及向量加法的交换律、结合律等基础知识.在求解时需将杂乱的向量运算式有序化处理,必要时也可化减为加,减低出错律.
题型2: 结合图型考查向量加、减法
[例3] (2008·广州市一模)在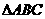 所在的平面上有一点
所在的平面上有一点 ,满足
,满足
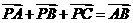 ,则
,则 与
与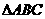 的面积之比是( )
的面积之比是( )
A. B.
B. C.
C. D.
D.
 [解题思路]: 本题中的已知向量都集中体现在三角形中.为此,可充分利用向量加减法的三角形法则实施求解.
[解题思路]: 本题中的已知向量都集中体现在三角形中.为此,可充分利用向量加减法的三角形法则实施求解.
[解析]由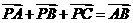 ,得
,得 ,
,
即 ,所以点
,所以点 是
是 边上的第二个三等分点,如图所示.
边上的第二个三等分点,如图所示.
故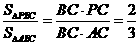 .
.
[名师指引]三角形中两边对应向量已知,可求第三边所对应的向量.值得注意的是,向量的方向不能搞错.当向量运算转化成代数式运算时,其运算过程可仿照多项式的加减运算进行.
[新题导练]
1. 判断下列命题是否正确,若不正确,请简述理由.
①向量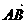 与
与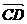 是共线向量,则A、B、C、D四点必在一直线上;
是共线向量,则A、B、C、D四点必在一直线上;
②单位向量都相等;
③任一向量与它的相反向量不相等;
④四边形ABCD是平行四边形的充要条件是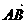 =
=
⑤模为0是一个向量方向不确定的充要条件;
⑥共线的向量,若起点不同,则终点一定不同.
解:①不正确.共线向量即平行向量,只要求方向相同或相反即可,并不要求两个向量 、
、 在同一直线上.
在同一直线上.
②不正确.单位向量模均相等且为1,但方向并不确定.
③不正确.零向量的相反向量仍是零向量,但零向量与零向量是相等的.
 ④、⑤正确.⑥不正确.如图
④、⑤正确.⑥不正确.如图 与
与 共线,虽起点不同,但其终点却相同.
共线,虽起点不同,但其终点却相同.
评述:本题考查基本概念,对于零向量、单位向量、平行向量、共线向量的概念特征及相互关系必须把握好.
3.重难点:.
问题1: 相等向量与平行向量的区别
答案:向量平行是向量相等的必要条件。
问题2:向量平行(共线)与直线平行(共线)有区别
答案:直线平行不包括共线(即重合),而向量平行则包括共线(重合)的情况。
问题3:对于两个向量平行的充要条件:
a∥b a=λb,只有b≠0才是正确的.而当b=0时,a∥b是a=λb的必要不充分条件.
a=λb,只有b≠0才是正确的.而当b=0时,a∥b是a=λb的必要不充分条件.
问题4;向量与有向线段的区别:
(1)向量是自由向量,只有大小和方向两个要素;与起点无关:只要大小和方向相同,则这两个向量就是相同的向量;
(2)有向线段有起点、大小和方向三个要素,起点不同,尽管大小和方向相同,也是不同的有向线段
★ 热 点 考 点 题 型 探 析★
考点一: 向量及与向量相关的基本概念
题型1. 概念判析
[例1]判断下列各命题是否正确
(1)零向量没有方向
(2)若
(3)单位向量都相等 (4) 向量就是有向线段
(5)两相等向量若共起点,则终点也相同
(6)若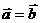 ,
, ,则
,则 ;
;
(7)若 ,
, ,则
,则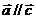 (8)若四边形ABCD是平行四边形,则
(8)若四边形ABCD是平行四边形,则
(9) 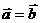 的充要条件是
的充要条件是 且
且 ;
;
[解题思路]:正确理解向量的有关概念,以概念为判断依据,或通过举反例说明。
解析:解:(1) 不正确,零向量方向任意, (2) 不正确,说明模相等,还有方向 (3) 不正确,单位向量的模为1,方向很多 (4) 不正确,有向线段是向量的一种表示形式 (5)正确, (6)正确,向量相等有传递性 (7)不正确,因若 ,则不共线的向量
,则不共线的向量 也有
也有 ,
, 。(8) 不正确, 如图
。(8) 不正确, 如图
 (9)不正确,当
(9)不正确,当 ,且方向相反时,即使
,且方向相反时,即使 ,也不能得到
,也不能得到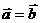 ;
;
[名师指引]对于有关向量基本概念的考查,可以从概念的特征入手,也可以从通过举出反例而排除或否定相关命题。
[新题导练]
2.难点:掌握向量加法的交换律、结合律,并会用它们进行向量化简与计算.
1.重点:理解向量及与向量相关的概念,掌握向量的几何表示,掌握向量的加法与减法,会正确运用三角形法则、平行四边形法则.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com