6.根据流程图可得结果为(　　 )

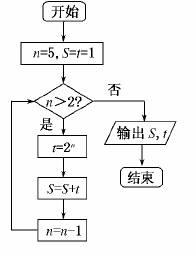
A.61,4　　　　　　　　　 B.57,2

C.49,16　　　　　　 　　 D.57,8

解析:运行程序:

n=5>2,t=2⁵=32,S=1+32=33,n=4>2,

t=2⁴=16,S=33+16=49,n=3>2,

t=2³=8,S=49+8=57,n=2=2结束,

∴输出的结果为S=57,t=8,故选D.

答案:D

二､填空题:(本大题共4小题,每小题6分,共24分,把正确答案填在题后的横线上.)

5.下列判断不正确的是(　　 )

A.画工序流程图类似于算法的流程图,要先把每一个工序逐步细化,按自上向下或自左到右的顺序

B.在工序流程图中可以出现循环回路,这一点不同于算法流程图

C.工序流程图中的流程线表示相邻两工序之间的衔接关系

D.工序流程图中的流程线都是有方向的指向线

解析:根据工序流程图的特点可知,A､C､D均正确.只有B不正确,故选B.

答案:B

4.下图中①､②､③､④依次为(　　 )

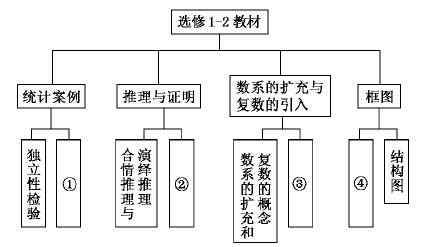
A.回归分析､复数代数形式的四则运算､直接证明与间接证明､流程图

B.回归分析､直接证明与间接证明､复数代数形式的四则运算､流程图

C.流程图､复数代数形式的四则运算､直接证明与间接证明､回归分析

D.流程图､直接证明与间接证明､复数代数形式的四则运算､回归分析

答案:B

2.如图是“集合”的知识结构图,如果要加入“子集”,则应该放在(　　 )

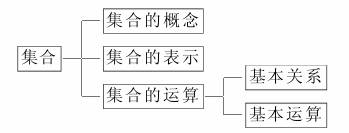
A.“集合的概念”的下位　　 　　　　　 B.“集合的表示”的下位

C.“基本关系”的下位　　　 　　　　　 D.“基本运算”的下位

解析:根据集合部分的结构,“子集”应在“基本关系”的下位,故选C.

答案:C

1.下列说法正确的是(　　 )

A.流程图只有1个起点和1个终点

B.程序框图只有1个起点和1个终点

C.工序图只有1个起点和1个终点

D.以上都不对

解析:由相关概念判断知只有关于程序框图的描述是对的,选B.

答案:B

13.已知复数z=1+i,求实数a,b,使得az+2b=(a+2z)².

分析:充分利用共轭复数的性质､复数相等的充要条件即可解出,在求解过程中,整体代入可获得简捷明快､别具一格的解法.

解:因为z=1+i,

所以az+2b=(a+2b)+(a-2b)i,(a+2z)²=(a²+4a)+4(a+2)i.

因为a,b都是实数,所以可得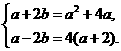

解得或

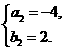即a=-2,b=-1或a=-4,b=2.

12.复数z₁=3+4i,z₂=0,z₃=c+(2c-6)i在复平面内对应的点分别为A､B､C,若∠BAC是钝角,求实数c的取值范围.

解:在复平面内三点坐标分别为A(3,4),B(0,0),C(c,2c-6),由∠BAC是钝角得<0,且B､A､C不共线,

由(-3,-4)·(c-3,2c-10)<0解得c>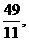

其中当c=9时,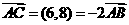 ,三点共线,故c≠9.

∴c的取值范围是c>且c≠9.

11.当实数m为何值时,z=lg(m²-2m-2)+(m²+3m+2)i

(1)为纯虚数;

(2)为实数;

(3)对应的点在复平面内的第二象限内.

解:(1)若z为纯虚数,

则有

即

⇒

∴m=3;

(2)若z为实数,则有

⇒m=-1或m=-2;

(3)若z对应的点在复平面内的第二象限,

则有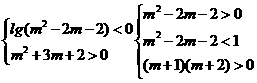

⇒

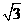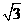⇒-1<m<1-或1+<m<3.

10.已知复数z=x+yi且|z-2|=则的最大值是________;最小值是________.

解析:∵|z-2|=,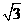

∴(x-2)²+y²=3,

则可看作是圆(x-2)²+y²=3上的点与原点连线的斜率,

设=k,则直线y=kx与圆相切时,k可以取到最大或最小值.

即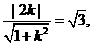解得或,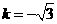

即最大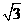值为,最小值为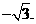

答案:

三､解答题:(本大题共3小题,11､12题13分,13题14分,写出证明过程或推演步骤.)