
题目列表(包括答案和解析)
13.已知集合A={x|-1≤x≤0},集合B={x|ax+b·2x-1<0,0≤a≤2,1≤b≤3}.
(1)若a,b∈N,求A∩B≠∅的概率;
(2)若a,b∈R,求A∩B=∅的概率.
解:(1)因为a,b∈N,(a,b)可取(0,1),(0,2),(0,3),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)共9组.
令函数f(x)=ax+b·2x-1,x∈[-1,0],
则f′(x)=a+bln2·2x.
因为a∈[0,2],b∈[1,3],所以f′(x)>0,
即f(x)在[-1,0]上是单调递增函数.
f(x)在[-1,0]上的最小值为-a+-1.
要使A∩B≠∅,只需-a+-1<0,即2a-b+2>0.
所以(a,b)只能取(0,1),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)共7组.
所以A∩B≠∅的概率为.
(2)因为a∈[0,2],b∈[1,3],所以(a,b)对应的区域为边长为2的正方形(如图),面积为4.
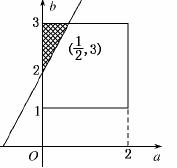
由(1)可知,要使A∩B=∅;
只需f(x)min=-a+-1≥0⇒2a-b+2≤0,所以满足A∩B=∅的(a,b)对应的区域是图中的阴影部分.
所以S阴影=×1×=,
所以A∩B=∅的概率为P==.
12.设有关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
解:记事件A为“方程x2+2ax+b2=0有实根”,
当a≥0,b≥0时,方程x2+2ax+b2=0有实根的充要条件为a≥b.
(1)基本事件共有12个:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),其中第一个数表示a的取值,第二个数表示b的取值.
事件A中包含9个基本事件,事件A发生的概率为
P(A)==.
(2)试验的全部结果所构成的区域为
{(a,b)|0≤a≤3,0≤b≤2}.
构成事件A的区域为
{(a,b)|0≤a≤3,0≤b≤2,a≥b},
所以所求的概率为
P(A)==.
11.汉字是世界上最古老的文字之一,字形结构体现着人类追求均衡对称、和谐稳定的天性.如图,三个汉字可以看成是轴对称图形.

(1)请再写出2个可看成轴对称图形的汉字;
(2)小敏和小慧利用“土”“口”“木”三个汉字设计一个游戏,规则如下:将这三个汉字分别写在背面都相同的三张卡片上,背面朝上,洗匀后抽出一张,放回洗匀后再抽出一张,若两次抽出的汉字能构成上下结构的汉字(如“土”“土”构成“圭”)则小敏获胜,否则小慧获胜.你认为这个游戏对谁有利?请用列表或画树状图的方法进行分析,并写出构成的汉字进行说明.
解:(1)如:田、日等;
(2)这个游戏对小慧有利.
每次游戏时,所有可能出现的如果如下(列表):
|
第二张卡片 第一张卡片 |
土 |
口 |
木 |
|
土 |
(土,土) |
(土,口) |
(土,木) |
|
口 |
(口,土) |
(口,口) |
(口,木) |
|
木 |
(木,土) |
(木,口) |
(木,木) |
总共有9种结果,且每种结果出现的可能性相同,其中能组成上下结构的汉字的结果有4种:(土,土)“圭”,(口,口)“吕”,(木,口)“杏”或“呆”,(口,木)“呆”或“杏”.所以小敏获胜的概率为,小慧获胜的概率为.所以这个游戏对小慧有利.
10.已知函数f(x)=2ax2-bx+1,若a是从区间[0,2]上任取的一个数,b是从区间[0,2]上任取的一个数,则此函数在[1,+∞)上递增的概率为________.
解析:令t=ax2-bx+1,函数f(x)在[1,+∞)上递增,根据复合函数单调性的判断方法,则t=ax2-bx+1须在[1,+∞)上递增,
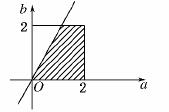
∴-≤1,即2a≥b.
由题意得
画出图示得阴影部分面积.
∴概率为P==.
答案:
9.任取一个三位正整数n,则对数log2n是一个正整数的概率是________.
解析:∵26=64,27=128,28=256,29=512,210=1024,
∴满足条件的正整数只有27,28,29三个,
∴所求的概率是P==.
答案:
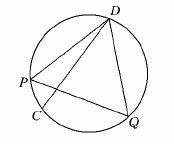
8.设D是半径为R的圆周上的一定点,在圆周上随机取一点C,连接CD得一弦,若A表示“所得弦的长大于圆内接等边三角形的边长”,则P(A)=________.
解析:如图所示,△DPQ为圆内接正三角形,当C点位于劣弧 上时,弦DC>PD,
上时,弦DC>PD,
∴P(A)=.
答案:
7.甲、乙两人玩数字游戏,先由甲心中任想一个数字记为a,再由乙猜甲刚才想的数字,把乙想的数字记为b,且a、b∈{1,2,3,4,5,6},若|a-b|≤1,则称“甲乙心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________.
解析:数字a,b的所有取法有62=36种,满足|a-b|≤1的取法有16种,所以其概率为P==.
答案:
6.4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( )
A. B.
C. D.
解析:从4张卡片中随机取2张共有6种取法,取得2张卡片上数字之和为奇数即{1,2},{1,4},{3,2},{3,4}四种,故其概率为=.故选C.
答案:C
5.如图所示,在边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为,则阴影区域的面积为( )
A. B.
C. D.
解析:正方形的面积为4,由=,知阴影区域的面积为,选B.
答案:B
4.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注数字外完全相同,现从中随机取2个小球,则取出的小球标注的数字之和为3或6的概率是( )
A. B.
C. D.
解析:随机从袋子中取2个小球的基本事件为(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共有10种,其中数字之和为3或6的有(1,2),(1,5),(2,4),∴数字之和为3或6的概率是P=.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com