
题目列表(包括答案和解析)
4.把等腰直角△ABC沿斜边上的高AD折成直二面角B-AD-C,则BD与平面ABC所成角的正切值为 ( )
A. B. C.1 D.
解析:如图,在面ADC中,过D作DE⊥AC,交AC于点E.
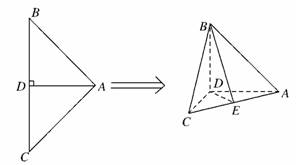
连接BE,因为二面角B-AD-C为直二面角,所以BD⊥平面ADC,故BD⊥AC.
由以上可知,AC⊥平面BDE,所以平面BDE⊥平面ABC,故∠DBE就是BD与平面ABC所成角,在Rt△DBE中,易求tan∠DBE=,故选B.
答案:B
3.(改编题)设P是△ABC所在平面外一点,P到△ABC各顶点的距离相等,而且P到△ABC各边的距离也相等,那么△ABC( )
A.是非等腰的直角三角形
B.是等腰直角三角形
C.是等边三角形
D.不是A、B、C所述的三角形
解析:设O是点P在平面ABC内的射影,因为P到△ABC各顶点的距离相等,所以O是三角形的外心,又P到△ABC各边的距离也相等,所以O是三角形的内心,故△ABC是等边三角形,选C.
答案:C
2.若m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题中的真命题是( )
A.若m⊂β,α⊥β,则m⊥α
B.若α∩γ=m,β∩γ=n,m∥n,则α∥β
C.若m⊥β,m∥α,则α⊥β
D.若α⊥γ,α⊥β,则β⊥γ
解析:两平面垂直并不能得到一个平面内的任一直线都与另一平面垂直,故A为假命题;以三棱柱的侧面和侧棱为例知B为假命题;若α⊥γ,α⊥β,则β⊥γ或β∥γ,故D为假命题;若m∥α,则α中必存在直线l与m平行,又m⊥β,∴l⊥β,故α⊥β,故选C.
答案:C
1.教室内任意放一支笔直的铅笔,则在教室的地面上必存在直线与铅笔所在的直线( )
A.平行 B.相交
C.异面 D.垂直
解析:这支铅笔与地面存在三种位置关系,若在地面内,则C排除;若与地面平行则B排除;若与地面相交,则A排除,选D.
答案:D
13.要分析学生初中升学的数学成绩对高一年级数学学习有什么影响,在高一年级学生中随机抽选10名学生,分析他们入学的数学成绩和高一年级期末数学考试成绩,如下表所示:
|
x |
63 |
67 |
45 |
88 |
81 |
71 |
52 |
99 |
58 |
76 |
|
y |
65 |
78 |
52 |
82 |
82 |
89 |
73 |
98 |
56 |
75 |
表中x是学生入学数学成绩,y是指高一年级期末考试数学成绩.
(1)画出散点图;
(2)求回归直线方程;
(3)若某学生王明亮的入学数学成绩为80分,试预测他在高一年级期末考试中的数学成绩为多少?
解:(1)作出散点图如图所示,从散点图可以看出,这两个变量具有线性相关关系.
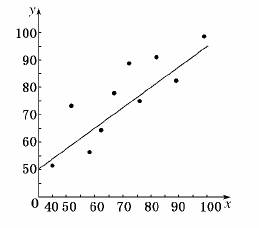
(2)
|
i |
xi |
yi |
x |
y |
xiyi |
|
1 |
63 |
65 |
3969 |
4225 |
4095 |
|
2 |
67 |
78 |
4489 |
6084 |
5226 |
|
3 |
45 |
52 |
2025 |
2704 |
2340 |
|
4 |
88 |
82 |
7744 |
6724 |
7216 |
|
5 |
81 |
82 |
6561 |
6724 |
6642 |
|
6 |
71 |
89 |
5041 |
7921 |
6319 |
|
7 |
52 |
73 |
2704 |
5329 |
3796 |
|
8 |
99 |
98 |
9801 |
9604 |
9702 |
|
9 |
58 |
56 |
3364 |
3136 |
3248 |
|
10 |
76 |
75 |
5776 |
5625 |
5700 |
|
合计 |
700 |
750 |
51474 |
58076 |
54284 |
可求得=(63+67+…+76)=70,
=(65+78+…+75)=75.
b=≈0.721,
∴a=75-0.721×70≈24.53.
所求的线性回归方程为
=0.721x+24.53.
(3)若王明亮入学数学成绩为80分,代入上面的线性回归方程
=0.721x+24.53可得≈82分.
12.据报道,某公司的33名职工的月工资(以元为单位)如下:
|
职务 |
董事长 |
副董事长 |
董事 |
总经理 |
经理 |
管理员 |
职员 |
|
人数 |
1 |
1 |
2 |
1 |
5 |
3 |
20 |
|
工资 |
5500 |
5000 |
3500 |
3000 |
2500 |
2000 |
1500 |
(1)求该公司职工月工资的平均数、中位数、众数;
(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平?结合此问题谈一谈你的看法.
解:(1)平均数是=1500+
≈1500+591=2091(元).
中位数是1500元,众数是1500元.
(2)平均数是′=1500+
≈1500+1788=3288(元).
中位数是1500元,众数是1500元.
(3)在这个问题中,中位数或众数均能反映该公司员工的工资水平.因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差数大,所以平均数不能反映这个公司员工的工资水平.
11.一个地区共有5个乡镇30000人,其中人口比例为3?2?5?1?4,要从这30000人中抽取300个人进行某种传染病分析,因考虑该传染病与不同地理位置及水土有关,问应采取什么样的抽样方法?写出抽样过程.
解:应采用分层抽样的方法.
具体抽样过程如下:
(1)计算抽样比:=;
(2)计算各乡镇人口数分别为:×30000=6000,×30000=4000,×30000=10000,×30000=2000,×30000=8000;
(3)计算各乡镇抽取的人口数分别为:6000×=60,4000×=40,10000×=100,2000×=20,8000×=80;
(4)用系统抽样的方法依次从五个乡镇中抽出60人,40人,100人,20人,80人;
(5)将抽取的个体合在一起,就构成所要抽取的一个样本.
10.某肉食鸡养殖小区某种病的发病鸡只数呈上升趋势,统计近4个月这种病的新发病鸡只数的线性回归分析如下表所示:

如果不加控制,仍按这个趋势发展下去,请预测从9月初到12月底的4个月时间里,该养殖小区这种病的新发病鸡总只数约为________.
解析:由上表可得:=94.7x+1924.7,当x分别取9,10,11,12时,得估计值分别为:2777,2871.7,2966.4,3061.1,则总只数约为2777+2871.7+2966.4+3061.1≈11676.
答案:11676
9.某地教育部门为了调查学生在数学答卷中的有关信息,从上次考试的10000名考生的数学试卷中用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图),则10000人的数学成绩在[140,150]段的约是________人.
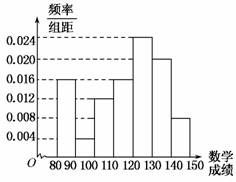
解析:设500人的数学成绩在[140,150]段的人数为x,10000人的数学成绩在[140,150]段的人数为n.
由样本频率分布直方图知数学成绩在[140,150]段的频率最小矩形的面积,即为0.008×10=0.08=,∴x=40.又样本的个数占总个数的,即每组的抽样比为,
∴=,∴n=800.
∴10000人的数学成绩在[140,150]段的约是800人.
答案:800
8.已知总体的各个体的值由小到大依次为2,3,3,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5,若要使该总体的方差最小,则a,b的取值是________和________.
解析:由题意a+b=21,故平均数=10.
欲使方差最小,只需使(a-10)2+(b-10)2最小,
又∵(a-10)2+(b-10)2=a2+b2-20(a+b)+200=a2+b2-220=(a+b)2-2ab-220=221-2ab≥221-22,当且仅当a=10.5,b=10.5时最小,故a=10.5,b=10.5时,s2最小.
答案:10.5 10.5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com