
题目列表(包括答案和解析)
1.将一个长方体沿从同一个顶点出发的三条棱截去一个棱锥,棱锥的体积与剩下的几何体的体积之比为( )
A.1:2 B.1:3
C.1:4 D.1:5
解析:设长方体同一顶点引出的三条棱长分别是a,b,c,则棱锥的体积V1= ×
×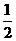 abc=
abc=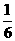 abc.长方体的体积V=abc,剩下的几何体的体积为V2=abc-
abc.长方体的体积V=abc,剩下的几何体的体积为V2=abc-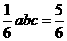 abc,所以V1:V2=1:5,故选D.
abc,所以V1:V2=1:5,故选D.
答案:D
13.如图,在矩形ABCD中,AB=2BC,P、Q分别为线段AB、CD的中点,EP⊥平面ABCD.

(1)求证:DP⊥平面EPC;
(2)问在EP上是否存在点F使平面AFD⊥平面BFC?若存在,求出的值.
解:(1)证明:∵EP⊥平面ABCD,
∴EP⊥DP,
又ABCD为矩形,AB=2BC,
P、Q为AB、CD中点,
∴PQ⊥DC且PQ=DC,
∴DP⊥PC,
∵EP∩PC=P,
∴DP⊥平面EPC.
(2)如图,假设存在F使平面AFD⊥平面BFC,
∵AD∥BC,AD⊄平面BFC,
BC⊂平面BFC,
∴AD∥平面BFC,
∴AD平行于平面AFD与平面BFC的交线l.
∵EP⊥平面ABCD,
∴EP⊥AD,而AD⊥AB,AB∩EP=P,
∴AD⊥平面EAB,
∴l⊥平面FAB,
∴∠AFB为平面AFD与平面BFC所成二面角的平面角,
∵P是AB的中点,且FP⊥AB,
∴当∠AFB=90°时,FP=AP,
∴当FP=AP,即=1时,平面AFD⊥平面BFC.
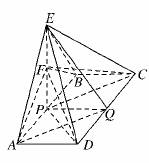
12.如图所示,已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且==λ(0<λ<1).

(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD?
解:(1)证明:∵AB⊥平面BCD,
∴AB⊥CD,
∵CD⊥BC且AB∩BC=B,
∴CD⊥平面ABC.
又==λ(0<λ<1),
∴不论λ为何值,恒有EF∥CD,
∴EF⊥平面ABC,又∵EF⊂平面BEF,
∴不论λ为何值,恒有平面BEF⊥平面ABC.
(2)由(1)知,BE⊥EF,
又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC,
∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴BD=,AB=tan60°=,
∴AC==,
由AB2=AE·AC得AE=,
∴λ==,
故当λ=时,平面BEF⊥平面ACD.
11.如图(1),等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点,如图(2),将△ABE沿AE折起,使二面角B-AE-C成直二面角,连接BC,BD,F是CD的中点,P是棱BC的中点.

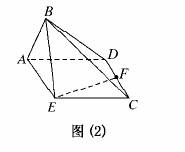
(1)求证:AE⊥BD;
(2)求证:平面PEF⊥平面AECD;
(3)判断DE能否垂直于平面ABC?并说明理由.
分析:由条件可知△ABE为正三角形,要证AE⊥BD,可证明AE垂直于BD所在的平面BDM,即证AE⊥平面BDM;可用判定定理证明平面PEF⊥平面AECD;对于第(3)问可采用反证法证明.
解: (1)证明:取AE中点M,连接BM,DM.
∵在等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点,
△ABE与△ADE都是等边三角形.
∴BM⊥AE,DM⊥AE. 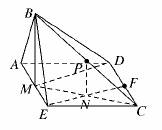
∵BM∩DM=M,BM,DM⊂平面BDM.
∴AE⊥平面BDM.
∵BD⊂平面BDM,∴AE⊥BD.
(2)证明:连接CM,EF交于点N,连接PN,如图.
∵ME∥FC,且ME=FC,
∴四边形MECF是平行四边形.
∴N是线段CM的中点.
∵P是线段BC的中点,∴PN∥BM.
∵BM⊥平面AECD,∴PN⊥平面AECD.
又∵PN⊂平面PEF,
∴平面PEF⊥平面AECD.
(3)DE与平面ABC不垂直,
证明:假设DE⊥平面ABC,则DE⊥AB,
∵BM⊥平面AECD.∴BM⊥DE.
∵AB∩BM=B,AB,BM⊂平面ABE,
∴DE⊥平面ABE.
∴DE⊥AE,这与∠AED=60°矛盾.
∴DE与平面ABC不垂直.
评析:翻折与展开是一个问题的两个方面,不论是翻折还是展开,均要注意平面图形与立体图形中各个对应元素的相对变化,元素间大小与位置关系,哪些不变,哪些变化,这是至关重要的.
10.(2010·东城目标检测)过正三棱锥的侧棱与底面中心作截面,已知截面是等腰三角形,若侧面与底面所成的角为θ,则cosθ的值是 .
解析:本题考查二面角的求法.
设侧面与底面所成的角为θ,如图,

O为中心,∴θ=∠SPB,又△SPB为等腰三角形,有两种情况:
(1)SP=PB,∴OP=SP⇒cosθ==;
(2)SB=PB,则SP==
== =AC,
又BP=AC,
OP=BP,∴cosθ==,
综上可得:cosθ的值是或.
答案:或
9.α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:①m⊥n;②α⊥β;③n⊥β;④m⊥α.
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题: .
解析:由题意构作四个命题:
(1)①②③⇒④;(2)①②④⇒③;(3)①③④⇒②;(4)②③④⇒①.
易判断(3)、(4)为真,应填m⊥α,n⊥β,α⊥β⇒m⊥n(或m⊥n,m⊥α,n⊥β⇒α⊥β).
答案:①③④⇒②;②③④⇒①
评析:本题为条件和结论同时开放的新颖试题.
8.如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF= 时,CF⊥平面B1DF.

解析:由题意易知,B1D⊥平面ACC1A1,所以B1D⊥CF.
要使CF⊥平面B1DF,
只需CF⊥DF即可.
令CF⊥DF,设AF=x,
则A1F=3a-x.
由Rt△CAF∽Rt△FA1D,得=,
即=,
整理得x2-3ax+2a2=0,
解得x=a或x=2a.
答案:a或2a
7.正四棱锥S-ABCD的底面边长为2,高为2,E是边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为 .
解析:如图,取CD的中点F、SC的中点G,连接EF,EG,FG,EF交AC于点H,易知AC⊥EF,又GH∥SO,

∴GH⊥平面ABCD,
∴AC⊥GH,∴AC⊥平面EFG,
故点P的轨迹是△EFG,
其周长为+.
答案:+
6.(2010·郑州质检)在边长为1的菱形ABCD中,∠ABC=60°,将菱形沿对角线AC折起,使折起后BD=1,则二面角B-AC-D的余弦值为( )

A. B. C. D.
解析:在原图中连接AC与BD交于O点,则AC⊥BD,在折起后的图中,由四边形ABCD为菱形且边长为1,则DO=OB=,由于DO⊥AC,因此∠DOB就是二面角B-AC-D的平面角,由BD=1
得cos∠DOB===,
故选A.
答案:A
5.如图,已知△ABC为直角三角形,其中∠ACB=90°,M为AB的中点,PM垂直于△ACB所在平面,那么( )

A.PA=PB>PC
B.PA=PB<PC
C.PA=PB=PC
D.PA≠PB≠PC
解析:∵M为AB的中点,△ACB为直角三角形,∴BM=AM=CM,又PM⊥平面ABC,∴Rt△PMB≌Rt△PMA≌Rt△PMC,故PA=PB=PC.选C.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com