
题目列表(包括答案和解析)
5.为了得到函数 的图象,可以把函数
的图象,可以把函数 的图象 ( )
的图象 ( )
A.向左平移3个单位长度 B.向右平移3个单位长度
C.向左平移1个单位长度 D.向右平移1个单位长度
4. 函数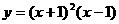 在
在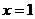 处的导数等于 ( )
处的导数等于 ( )
A.1 B.2 C.3 D.4
3.正三棱柱侧面的一条对角线长为2,且与底面成45°角,则此三棱柱的体积为 ( )
A.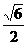 B.
B. 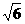 C.
C. D.
D. 
2.函数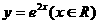 的反函数为 ( )
的反函数为 ( )
A.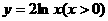 B.
B.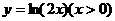
C.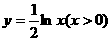 D.
D.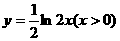
 一项是符合题目要求的.
一项是符合题目要求的.
1.设集合U={1,2,3,4,5},集合M={0,3,5},N={1,4,5},则M∩( U N)=
( )
A.{5} B.{0,3} C.{0,2,3,5} D. {0,1,3,4,5}
(17)(本小题满分12分)
解方程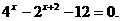
(18) (本小题满分12分)
已知α为锐角,且 的值.
的值.
(19) (本上题满分12分)
设数列 是公差不为零的等差数列,Sn是数列
是公差不为零的等差数列,Sn是数列 的前n项和,且
的前n项和,且
 ,求数列
,求数列 的通项公式.
的通项公式.
20.(本小题满分12分)
某村计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,沿左、右两侧与后侧
内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地。当矩形温室的边长各为多少
时,蔬菜的种植面积最大?最大种植面积是多少?
(21) (本小题满分12分)
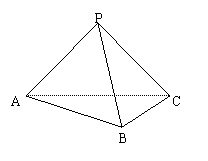
三棱锥P-ABC中,侧面PAC与底面ABC垂直,PA=PB=PC=3.
(1) 求证AB⊥BC;
(2) 如果AB=BC=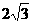 ,求侧面PBC与侧面PAC所成二面角的大小.
,求侧面PBC与侧面PAC所成二面角的大小.
(22)(本小题满分14分)
设椭圆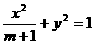 的两个焦点是
的两个焦点是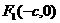 与
与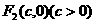 ,且椭圆上存在点P,
,且椭圆上存在点P,
使得直线PF2与直线PF2垂直.
(1)求实数m的取值范围;
(2)设L是相应于焦点F2的准线,直线PF2与L相交于点Q. 若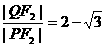 ,
,
求直线PF2的方程.
2004年普通高等学校招生全国统一考试
(13) 函数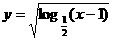 的定义域是
.
的定义域是
.
(14) 用平面α截半径为R的球,如果球心到平面α的距离为 ,那么截得小圆的面积与球
,那么截得小圆的面积与球
的表面积的比值为 .
(15) 函数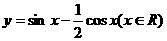 的最大值为
.
的最大值为
.
(16) 设P为圆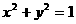 上的动点,则点P到直线
上的动点,则点P到直线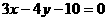 的距离的最小值为
的距离的最小值为
.
(1)设集合 ,
, ,
,
则集合 中元素的个数为( )
中元素的个数为( )
A.1 B.2 C.3 D.4
(2)函数 的最小正周期是( )
的最小正周期是( )
A.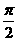 B.
B.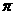 C.
C.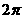 D.
D.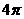
(3) 记函数 的反函数为
的反函数为 ,则
,则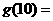 ( )
( )
A. 2
B.  C. 3 D.
C. 3 D. 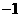
(4)
等比数列 中,
中,
 ,则
,则 的前4项和为( )
的前4项和为( )
A. 81 B. 120 C.168 D. 192
(5) 圆 在点
在点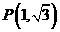 处的切线方程是( )
处的切线方程是( )
A.
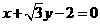 B.
B. 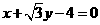
C. 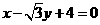 D.
D. 
(6)  展开式中的常数项为( )
展开式中的常数项为( )
A. 15 B.  C.
C.  20 D.
20 D. 
(7)
设复数 的幅角的主值为
的幅角的主值为 ,虚部为
,虚部为 ,则
,则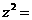 ( )
( )
A.
 B.
B. 
C.  D.
D. 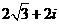
(8)
设双曲线的焦点在 轴上,两条渐近线为
轴上,两条渐近线为 ,则双曲线的离心率
,则双曲线的离心率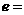 ( )
( )
A. 5 B.  C.
C. 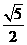 D.
D.
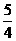
(9) 不等式 的解集为( )
的解集为( )
A. 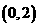 B.
B. 
C.
 D.
D. 
(10) 正三棱锥的底面边长为2,侧面均为直角三角形,则此三棱锥的体积为( )
A.  B.
B.
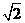 C.
C.  D.
D. 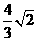
(11) 在 中,
中, ,则边
,则边 上的高为( )
上的高为( )
A.  B.
B. 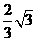 C.
C. 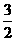 D.
D.
(12) 4名教师分配到3所中学任教,每所中学至少1名教师,则不同的分配方案共有( )
A. 12 种 B. 24 种 C 36 种 D. 48 种
第Ⅱ卷
22.(本小题满分14分)
给定抛物线C: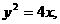 F是C的焦点,过点F的直线
F是C的焦点,过点F的直线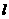 与C相交于A、B两点.
与C相交于A、B两点.
(Ⅰ)设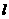 的斜率为1,求
的斜率为1,求 夹角的大小;
夹角的大小;
(Ⅱ)设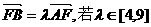 ,求
,求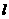 在
在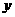 轴上截距的变化范围.
轴上截距的变化范围.
2004年普通高等学校招生全国统一考试
21.(本小题满分12分)
若函数 在区间(1,4)内为减函数,在区间
在区间(1,4)内为减函数,在区间
(6,+∞)上为增函数,试求实数a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com