4.若2－m与|m|－3异号，则m的取值范围是

A.m＞3　　 　　　　　　　　　　　　　　B.－3＜m＜3

C.2＜m＜3　　　　 　　　　　　　　　　D.－3＜m＜2或m＞3

3.设f(x)(x∈R)是以3为周期的奇函数，且f(1)＞1,f(2)=a则

A.a＞2　　　　　 　　B.a＜－2　　　　　　 C.a＞1　 　　　　　D.a＜－1

2.在锐角三角形中，A＞B是sinA＞sinB的

A.充分不必要条件　　 　　　　　　　　　　B.必要不充分条件

C.充要条件　　　 　　　　　　　　　　　D.既不充分也不必要条件

1.设集合M={a,b},则满足M∪N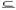{a,b,c}的集合N的个数为

A.1　　　　　　 　　　B.4　　 　　　　　　C.7　 　　　　　　　D.8

22.(本小题满分14分)

有一条生产流水线，由于改进了设备，预计第一年产量的增长率为150%，以后每年的增长率是前一年的一半，设原来的产量为a.

(1)写出改进设备后的第一年，第二年，第三年的产量，并写出第n年与第n-1年(n≥2,n∈N⁺)的产量之间的关系式；

(2)由于设备不断老化，估计每年将损失年产量的10%，照这样下去，以后每年的产量是否始终是逐年提高？若是，请给予证明；若不是，请说明从第几年起，产量将比上一年减少.

21.(本小题满分12分)

椭圆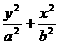=1(a＞b＞0)的两焦点为F₁(0,－c),F₂(0,c)(c＞0),离心率e=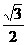,焦点到椭圆上点的最短距离为2-.

(1)求椭圆的方程；

(2)设P、Q为椭圆与直线y=x+1两个交点，求tanPOQ的值.

20.(本小题满分12分)

已知二次函数f(x)=ax²+bx(a,b为常数且a≠0)满足条件：

f(－x+5)=f(x－3),且方程f(x)=x有等根.

(1)求f(x)的解析式；

(2)是否存在实数m,n(m＜n),使f(x)的定义域和值域分别是［m,n］和［3m,3n］?如果存在，求出m,n的值；若不存在，说明理由.

19.(本小题满分12分)

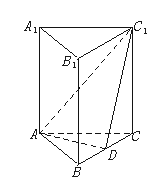
如图，正三棱柱各棱都相等，D是BC上一点，AD⊥C₁D

(1)求证：截面ADC₁⊥侧面BCC₁B₁；

(2)求二面角C-AC₁-D的大小.

18.(本小题满分12分)

设人的某一特征(如眼睛大小)是由他一对基因所决定，以d表示显性基因，r表示隐性基因，则具有dd基因的人为纯显性，具有rr基因的人为纯隐性，具有rd基因的人为混合性.纯显性与混合性都显露显性基因决定的某一特征，孩子从父母身上各得到一个基因，假定父母都是混合性，问：

(1)1个孩子有显性决定特征的概率是多少？

(2)2个孩子中至少有一个显性决定的特征的概率是多少？

17.(本小题满分12分)

已知函数f(x)=sin(x+)+sin(x－)+cosx+a(a∈R,a是常数).

(1)求函数f(x)的最小正周期；

(2)若x∈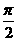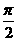［－,］时，f(x)的最大值为1，求a的值.