
题目列表(包括答案和解析)
10.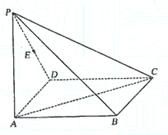 (本小题满分12分)(2005年高考·湖北卷·理20)
(本小题满分12分)(2005年高考·湖北卷·理20)
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=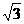 ,BC=1,PA=2,E为PD的中点. (Ⅰ)求直线AC与PB所成角的余弦值;
,BC=1,PA=2,E为PD的中点. (Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.
本小题主要考查线面关系和四棱锥等基础知识,同时考查空间想象能力和推理运算能力.
解法1:(Ⅰ)建立如图所示的空间直角坐标系,
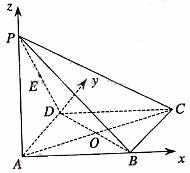 则A、B、C、D、P、E的坐标为A(0,0,0)、
则A、B、C、D、P、E的坐标为A(0,0,0)、
B(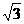 ,0,0)、C(
,0,0)、C(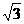 ,1,0)、D(0,1,0)、
,1,0)、D(0,1,0)、
P(0,0,2)、E(0,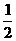 ,1),
,1),
从而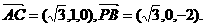
设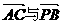 的夹角为θ,则
的夹角为θ,则
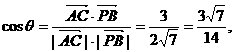
∴AC与PB所成角的余弦值为 .
.
(Ⅱ)由于N点在侧面PAB内,故可设N点坐标为(x,O,z),则
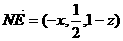 ,由NE⊥面PAC可得,
,由NE⊥面PAC可得,
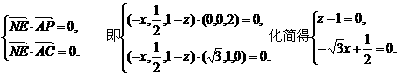 ∴
∴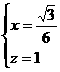
即N点的坐标为 ,从而N点到AB、AP的距离分别为1,
,从而N点到AB、AP的距离分别为1,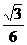 .
.
解法2:(Ⅰ)设AC∩BD=O,连OE,则OE//PB,
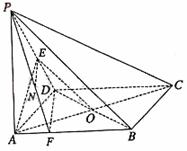 ∴∠EOA即为AC与PB所成的角或其补角.
∴∠EOA即为AC与PB所成的角或其补角.
在△AOE中,AO=1,OE=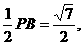
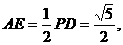
∴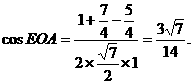
即AC与PB所成角的余弦值为 .
.
(Ⅱ)在面ABCD内过D作AC的垂线交AB于F,则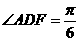 .
.
连PF,则在Rt△ADF中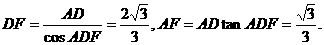
设N为PF的中点,连NE,则NE//DF,
∵DF⊥AC,DF⊥PA,∴DF⊥面PAC,从而NE⊥面PAC.
∴N点到AB的距离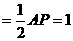 ,N点到AP的距离
,N点到AP的距离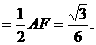
9. (本小题满分14分)(2005年高考·广东卷16)
(本小题满分14分)(2005年高考·广东卷16)
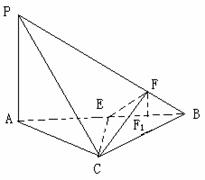
如图3所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=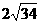 .F是线段PB上一点,
.F是线段PB上一点,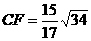 ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.
(Ⅰ)证明:PB⊥平面CEF;
(Ⅱ)求二面角B-CE-F的大小.
 (I)证明:∵
(I)证明:∵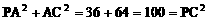 ,
,
∴△PAC是以∠PAC为直角的直角三角形.
同理可证:△PAB是以∠PAB为直角的直角三角形,
△PCB是以∠PCB为直角的直角三角形.
所以,PA⊥平面ABC.
又∵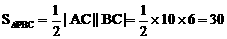 ,
,
而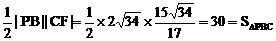 ,
,
故CF⊥PB,又已知EF⊥PB,
∴PB⊥平面CEF.
(II)由(I)知PB⊥CE, PA⊥平面ABC,
∴AB是PB在平面ABC上的射影,故AB⊥CE.
在平面PAB内,过F作FF1垂直AB交AB于F1,则FF1⊥平面ABC,
EF1是EF在平面ABC上的射影,∴EF⊥EC,
故∠FEB是二面角B-CE-F的平面角.
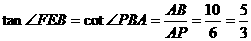 ,
,
二面角B-CE-F的大小为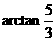 .
.
8.(本小题满分12分)(2005年高考·福建卷·理20文21)
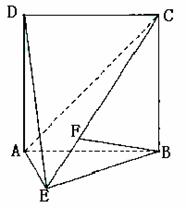 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的大小;
(Ⅲ)求点D到平面ACE的距离.
本小题主要考查直线、直线与平面、二面角及点到平面的距离等基础知识,考查空间想
象能力,逻辑思维能力与运算能力. 满分12分.
解法一:(Ⅰ)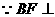 平面ACE.
平面ACE. 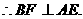
∵二面角D-AB-E为直二面角,且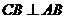 ,
,  平面ABE.
平面ABE.
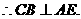
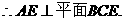
(Ⅱ)连结BD交AC于C,连结FG,
 ∵正方形ABCD边长为2,∴BG⊥AC,BG=
∵正方形ABCD边长为2,∴BG⊥AC,BG=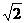 ,
,
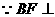 平面ACE,
平面ACE,
由三垂线定理的逆定理得FG⊥AC.
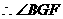 是二面角B-AC-E的平面角.
是二面角B-AC-E的平面角.
由(Ⅰ)AE⊥平面BCE, 又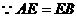 ,
,
∴在等腰直角三角形AEB中,BE=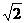 .
.
又 直角
直角
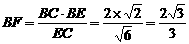 ,
,

∴二面角B-AC-E等于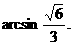
(Ⅲ)过点E作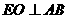 交AB于点O. OE=1.
交AB于点O. OE=1.
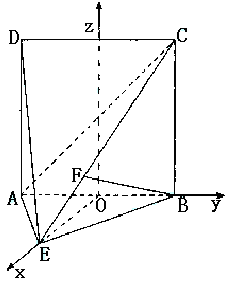 ∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD.
∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD.
设D到平面ACE的距离为h,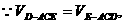

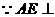 平面BCE,
平面BCE,
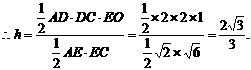
∴点D到平面ACE的距离为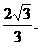
解法二:(Ⅰ)同解法一.
(Ⅱ)以线段AB的中点为原点O,OE所在直
线为x轴,AB所在直线为y轴,过O点平行
于AD的直线为z轴,建立空间直角坐标系
O-xyz,如图.
 面BCE,BE
面BCE,BE 面BCE,
面BCE,  ,
,
在 的中点,
的中点,
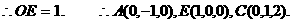
 设平面AEC的一个法向量为
设平面AEC的一个法向量为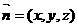 ,
,
则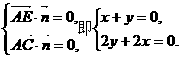
解得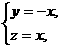
令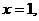 得
得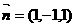 是平面AEC的一个法向量.
是平面AEC的一个法向量.
又平面BAC的一个法向量为 ,
,
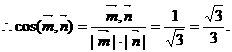
∴二面角B-AC-E的大小为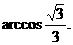
(III)∵AD//z轴,AD=2,∴ ,
,
∴点D到平面ACE的距离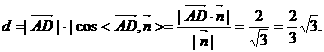
7.(本题满分12分)(2005年高考·上海卷·文17)
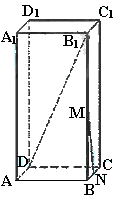 已知长方体
已知长方体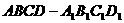 中,M、N分别是
中,M、N分别是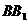 和BC的中点,AB=4,AD=2,
和BC的中点,AB=4,AD=2,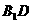 与平面ABCD所成角的大小为
与平面ABCD所成角的大小为 ,求异面直线
,求异面直线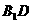 与MN所成角的大小.(结果用反三角函数值表示)
与MN所成角的大小.(结果用反三角函数值表示)
[解]联结B1C,由M、N分别是BB1和BC的中点,得B1C//MN
∴∠DB1C就是异面直线B1D与MN所成的角.
联结BD,在Rt△ABD中,可得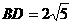 ,
,
又BB1⊥平面ABCD.
∠B1DB是B1D与平面ABCD的所成的角,
∴∠B1DB=60°.
在Rt△B1BD中,BB1=BDtan60°=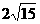 ,
,
又DC⊥平面BB1C1C, ∴DC⊥B1C,
在Rt△CB1C中,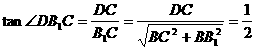
∴∠DB1C=
即异面直线B1D与MN所成角的大小为 .
.
6.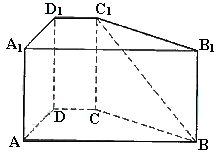 (本题满分12分)(2005年高考·上海卷·理17)
(本题满分12分)(2005年高考·上海卷·理17)
已知直四棱柱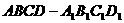 中,
中,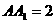 ,底面ABCD是直角梯形,∠A是直角,AB||CD,AB=4,AD=2,DC=1,求异面直线
,底面ABCD是直角梯形,∠A是直角,AB||CD,AB=4,AD=2,DC=1,求异面直线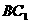 与DC所成角的大小.(结果用反三角函数值表示)
与DC所成角的大小.(结果用反三角函数值表示)
[解法一]由题意AB//CD,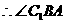 是异面直线BC1与DC所成的角.
是异面直线BC1与DC所成的角.
 连结AC1与AC,在Rt△ADC中,可得
连结AC1与AC,在Rt△ADC中,可得 ,
,
又在Rt△ACC1中,可得AC1=3.
在梯形ABCD中,过C作CH//AD交AB于H,
得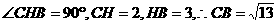
又在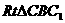 中,可得
中,可得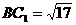 ,
,
在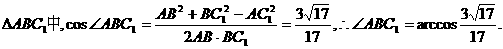
∴异而直线BC1与DC所成角的大小为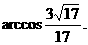
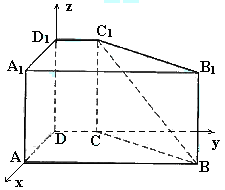 [解法二]如图,以D为坐标原点,分别以AD、DC、DD1所在直线为x、y、z轴建立直
[解法二]如图,以D为坐标原点,分别以AD、DC、DD1所在直线为x、y、z轴建立直
角坐标系.
则C1(0,1,2),B(2,4,0)
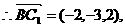
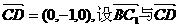 所成的角为
所成的角为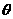 ,
,
则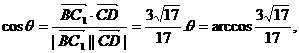
∴异面直线BC1与DC所成角的大小为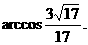
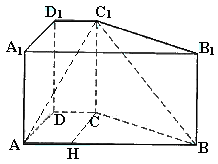
5. (本小题共14分)(2005年高考·北京卷·文16)
(本小题共14分)(2005年高考·北京卷·文16)
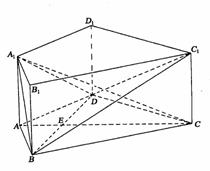
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
(Ⅰ)求证AC⊥BC1;
(Ⅱ)求证AC1//平面CDB1;
(Ⅲ)求异面直线AC1与B1C所成角的余弦值.
解法一:
(Ⅰ)∵直三棱柱ABC-A1B1C1底面三边长AC=3,BC=4,AB=5,
 ∴AC⊥BC,且BC1在平面ABC内的射影为BC,
∴AC⊥BC,且BC1在平面ABC内的射影为BC,
∴AC⊥BC1.
(Ⅱ)设CB1与C1B的交点为E,连结DE,
∵D是AB的中点,E是BC1的中点,
∴DE//AC1,
∵DE 平面CDB1,AC1
平面CDB1,AC1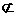 平面CDB1,
平面CDB1,
∴AC1//平面CDB1.
(Ⅲ)∵DE//AC1,∴∠CED为AC1与B1C所成的角,
在△CED中,ED =
=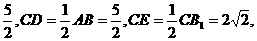
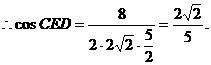
∴异面直线AC1与B1C所成角的余弦值为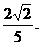
解法二:
∵直三棱柱ABC-A1B1C1底面三边长AC=3,BC=4,AB=5,
∴AC,BC,C1C两两垂直.
如图,以C为坐标原点,直线CA,CB,CC1分别为x轴,
y轴,z轴,建立空间直角坐标系,
则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),
B1(0,4,4),D(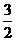 ,2,0).
,2,0).
(Ⅰ)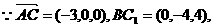
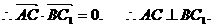
(Ⅱ)设CB1与C1B的交点为E,则E(0,2,2).
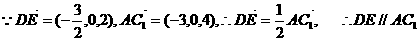

(Ⅲ)

∴异面直线AC1与B1C所成角的余弦值为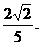
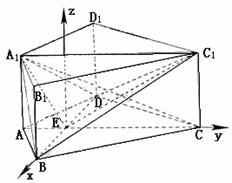
4.(本小题共14分)(2005年高考·北京卷·理16)
 如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=
如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=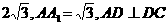 ,
,
AC⊥BD,垂足为E.
(Ⅰ)求证BD⊥A1C;
(Ⅱ)求二面角A1-BD-C1的大小;
(Ⅲ)求异面直线AD与BC1所成角的大小.
解法一:
(Ⅰ)在直四棱柱ABCD-A1B1C1D1中,
∵A1A⊥底面ABCD,
∴AC是A1C在平面ABCD上的射影,
∵BD⊥AC, ∴BD⊥A1C.
(Ⅱ)连结A1E,C1E,A1C1.
与(Ⅰ)同理可证BD⊥A1E,BD⊥C1E,
∴∠A1EC1二面角A1-BD-C1的平面角.
∵AD⊥DC, ∴∠A1D1C1=∠ADC=90°,
又A1D1=AD=2,D1C1=DC=2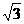 , AA1=
, AA1=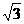 ,且AC⊥BD,
,且AC⊥BD,
∴A1C1=4,AE=1,EC=3, ∴A1E=2,C1E=2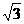 ,
,
在△A1EC1中,A1C12=A1E2+C1E2, ∴∠A1EC1=90°,
即二面角A1-BD-C1的大小为90°.
(Ⅲ)过B作BF//AD交AC于F,连结FC1,
则∠C1BF就是AD与BC1所成的角.
∵AB=AD=2,BD⊥AC,AE=1, ∴BF=2,EF=1,FC=2,BC=DC,
∴FC1=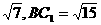 . 在△BFC1中,
. 在△BFC1中,
∴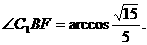
即异面直线AD与BC1所成角的大小为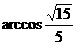 .
.
解法二:
(Ⅰ)同解法一.
(Ⅱ)如图,以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系.
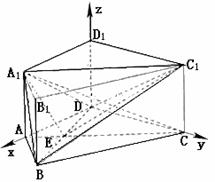 连结A1E,C1F,A1C1.
连结A1E,C1F,A1C1.
与(Ⅰ)同理可证,BD⊥A1E,BD⊥C1E,
∴∠A1EC1为二面角A1-BD-C1的平面角.
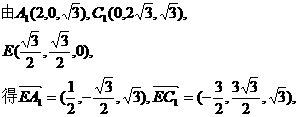
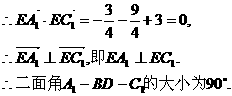
(Ⅲ)如图,由D(0,0,0),A(2,0,0),C1(0, ,
,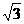 ,),B(3,
,),B(3,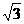 ,0)
,0)
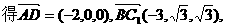
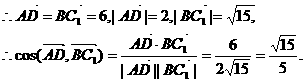
∴异面直线AD与BC1所成角的大小为arccos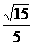 .
.
 解法三:
解法三:
(I)同解法一.
(II)如图,建立空间直角坐标系,坐标原点为E.
连结A1E,C1E,A1C1.
与(I)同理可证,BD⊥A1E,BD⊥C1E,
∴∠A1EC1为二面角A1-BD-C1的平面角.
由E(0,0,0),A1(0,-1,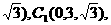
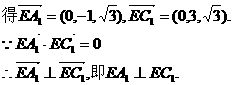
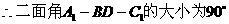 .
.
(Ⅲ)如图,由A(0,-1,0),D(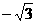 ,0,0),B(
,0,0),B(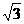 ,0,0),C1(0,3,
,0,0),C1(0,3,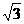 ).
).
得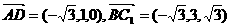 .
.
∵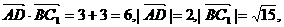
∴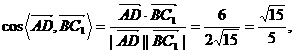
∴异面直线AD与BC1所成角的大小为arccos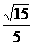 .
.
3. (本题满分14分) (2005年春考·上海卷19)本题共有2个小题,第1小题满分6分,第2小题满分8分.
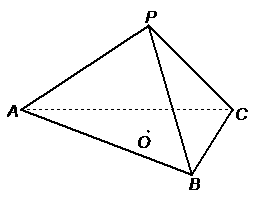
已知正三棱锥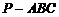 的体积为
的体积为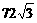 ,侧面与底面所成的二面角的大小为
,侧面与底面所成的二面角的大小为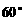 .
. (1)证明:
(1)证明: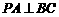 ;
;
(2)求底面中心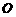 到侧面的距离.
到侧面的距离.
[证明](1)取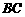 边的中点
边的中点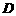 ,连接
,连接 、
、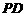 ,
,
则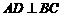 ,
,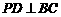 ,故
,故 平面
平面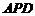 .
…… 4分
.
…… 4分
∴ 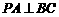 .
…… 6分
.
…… 6分
 [解](2)如图, 由(1)可知平面
[解](2)如图, 由(1)可知平面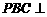 平面
平面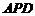 ,则
,则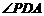 是侧面与底面所成二面角的平面角.
是侧面与底面所成二面角的平面角.
过点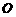 作
作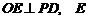 为垂足,则
为垂足,则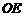 就是点
就是点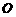 到侧面的距离.
…… 9分
到侧面的距离.
…… 9分
设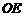 为
为 ,由题意可知点
,由题意可知点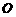 在
在 上,
上,
∴ 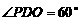 ,
,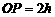 .
.
 , …… 11分
, …… 11分
∴  ,
,
∵ 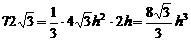 ,∴
,∴ 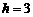 .
.
即底面中心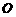 到侧面的距离为3.
…… 14分
到侧面的距离为3.
…… 14分
2. (本小题满分14分)(2005年春考·北京卷·文16)
(本小题满分14分)(2005年春考·北京卷·文16)
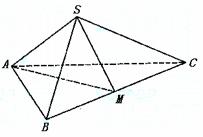
如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.求:
(Ⅰ)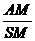 的值;
的值;
(Ⅱ)二面角S-BC-A的大小;
(Ⅲ)正三棱锥S-ABC的体积.
 本小题主要考查直线与平面的位置关系等基本知识,考查空间想象能力,罗辑思维能力和运算能力.满分14分.
本小题主要考查直线与平面的位置关系等基本知识,考查空间想象能力,罗辑思维能力和运算能力.满分14分.
解:(Ⅰ)∵SB=SC,AB=AC,M为BC中点,
∴SM⊥BC,AM⊥BC.
由棱锥的侧面积等于底面积的2倍,即
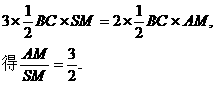
(Ⅱ)作正三棱锥的高SG,则G为正三角形ABC的中心,G在AM上,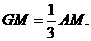
∵SM⊥BC,AM⊥BC,
∴∠SMA是二面角S-BC-A的平面角.
在Rt△SGM中,
∵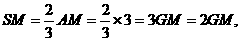
∴∠SMA=∠SMG=60°,
即二面角S-BC-A的大小为60°。
(Ⅲ)∵△ABC的边长是3,
∴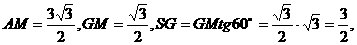
∴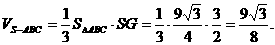
1.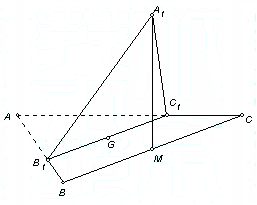 (本小题满分14分)(2005年春考·北京卷·理16)
(本小题满分14分)(2005年春考·北京卷·理16)
如图,正三角形ABC的边长为3,过其中心G作BC边的平行线,分别交AB、AC于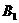 、
、 .将
.将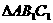 沿
沿 折起到
折起到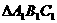 的位置,使点
的位置,使点 在平面
在平面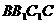 上的射影恰是线段BC的中点M.求:
上的射影恰是线段BC的中点M.求:
(1)二面角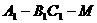 的大小;
的大小;
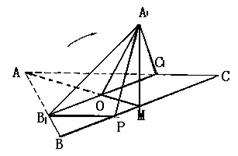 (2)异面直线
(2)异面直线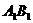 与
与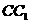 所成角的大小(用反三角函数表示).
所成角的大小(用反三角函数表示).
本小题主要考查直线与平面的位置关系等基本知识,考查空间想象能力,罗辑思维能力和运算能力.满分14分.
解(Ⅰ)连接AM,A1G
∵G是正三角形ABC的中心,
且M为BC的中点,
∴A,G,M三点共线,AM⊥BC.
∵B1C1∥BC,
∴B1C1⊥AM于G,
即GM⊥B1C1,GA1⊥B1C1,
∴∠A1GM是二面角A1-B1C1-M的平面角.
∵点A1在平面BB1C1C上的射影为M,
∴A1M⊥MG,∠A1MG=90°
在Rt△A1GM中,由A1G=AG=2GM得∠A1GM=90°
即二面角A1-B1C1-M的大小是60°
(Ⅱ)过B1作C1C的平行线交BC于P,则∠A1B1P等于异面直线A1B1与CC1所成的角.
由PB1C1C是平行四边形得B1P=C1C=1=BP,
PM=BM-BP= A1B1=AB1=2.
A1B1=AB1=2.
∵A1M⊥面BB1C1C于M,
∴A1M⊥BC,∠A1MP=90°.
在Rt△A1GM中,A1M=A1G·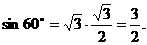
在Rt△A1MP中,
在△A1B1P中,由余弦定理得
 ,
,
∴异面直线A1B1与CC1所成角的大小为arccos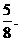
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com