
题目列表(包括答案和解析)
5.P为椭圆 =1上一点,F1、F2为焦点,如果∠PF1F2=75°,∠PF2F1=15°,则椭圆的离心率为
=1上一点,F1、F2为焦点,如果∠PF1F2=75°,∠PF2F1=15°,则椭圆的离心率为
A. B.
B. C.
C.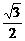 D.
D.
4.空间四边形四条边所在的直线中,互相垂直的直线最多有
A.2对 B.3对 C.4对 D.5对
3.正项等比数列{an}满足:a2·a4=1,S3=13,bn=log3an,则数列{bn}的前10项的和是
A.65 B.-65 C.25 D.-25
2.已知向量a=(cos75°,sin75°),b=(cos15°,sin15°),那么|a-b|的值是
A.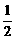 B.
B. C.
C.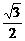 D.1
D.1
1.命题p:a2+b2<0(a,b∈R);命题q:a2+b2≥0(a,b∈R),下列结论正确的是
A.“p或q”为真 B.“p且q”为真
C.“非p”为假 D.“非q”为真
20.(本小题满分16分)
已知f(x)=a0+a1x+a2x2+…+anxn(n∈N*),且y=f(x)的图象经过点(1,n2),数列{an}为等差数列.
(1)求数列{an}的通项公式;
(2)当n为奇数时,设g(x)=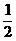 [f(x)-f(-x)],是否存在自然数m和M,使不等式m<g(
[f(x)-f(-x)],是否存在自然数m和M,使不等式m<g(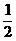 )<M恒成立?若存在,求出M-m的最小值;若不存在,说明理由.
)<M恒成立?若存在,求出M-m的最小值;若不存在,说明理由.
19.(本小题满分14分)
设f(x)是定义在[-1,1]上的偶函数,f(x)与g(x)的图象关于直线x=1对称,且当x∈[2,3]时,g(x)=a(x-2)-2(x-2)3(a为常数).
(1)求f(x)的解析式;
(2)若f(x)在[0,1]上是增函数,求a的取值范围;
(3)若a∈(-6,6),问能否使f(x)最大值为4.
18. (本小题满分13分)
(本小题满分13分)
已知△OFQ的面积为2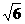 ,且
,且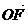 ·
· =m,
=m,
(1)设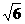 <m<4
<m<4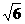 ,求向量
,求向量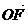 与
与 的夹角θ的取值范围;
的夹角θ的取值范围;
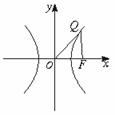
(2)设以O为中心,F为焦点的双曲线经过点Q(如图),|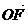 |=c,m=(
|=c,m=(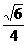 -1)c2,当|
-1)c2,当| |取最小值时,求此双曲线的方程.
|取最小值时,求此双曲线的方程.
17. (本小题满分13分)
(本小题满分13分)
如右图α-l-β是120°的二面角,A、B两点在棱l上,AB=2,D在α内,三角形ABD是等腰直角三角形,∠DAB=90°,C在β内,三角形ABC是等腰直角三角形,∠ACB=90°.
(1)求三棱锥D-ABC的体积;
(2)求二面角D-AC-B的大小.
(3)求异面直线AB、CD所成的角.
16.(本小题满分12分)
已知△ABC的面积为1,tanB=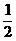 ,tanC=-2,求△ABC的边长及tanA.
,tanC=-2,求△ABC的边长及tanA.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com