
题目列表(包括答案和解析)
(二)、试卷结构:
第一卷:选择题,第二卷:非选择题
全国1、2、3卷和辽宁、湖北、江西、山东、福建卷:
选择题12道,填空题 4道,解答题6道。
北京:20道题,选择题8道,填空题 6道,解答题 6道。
上海:22道题,选择题4道,填空题 12道,解答题 6道。
江苏:23题,选择题12道,填空题 6道,解答题 5道。
湖南:21题,选择题10道,填空题 5道,解答题 6道。 广东,浙江:20道题,选择题10道,填空题 4道,解答题 6道
重庆,天津:22道题,选择题10道,填空题 6道,解答题 6道
(一)、试卷种类
全国1卷 : 河北、河南、山西、安徽、海南;
全国2卷 :黑龙江、吉林、广西;
全国3卷: 四川、云南、贵州、甘肃、新疆、青海、宁夏、陕西、西藏等。
十四个自主省市:
北京、上海、天津、重庆、福建、江苏、浙江、辽宁、广东、湖南、湖北、江西、山东、安徽(只有外语自主命题)。
(除辽宁、江苏、广东外数学都是文理分卷,共29份)
0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。
(I)求ξ的分布列及数学期望;
(II)记“函数试题详情
22.(本小题满分14分)
(理)已知函数
(1)求函数 的最大值;
的最大值;
(2)当 时,求证
时,求证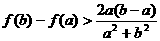 .
.
(文)设函数
(1)求函数f(x)的单调区间,并求函数f(x)的极大值和极小值;
(2)当x∈[a+1, a+2]时,不等 ,求a的取值范围.
,求a的取值范围.
21.(本小题满分12分)平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,
-2),点C满足 、
、
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线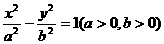 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: .
.
20.(本小题满分12分)如图,在底面是菱形的四棱锥P-ABCD中,
∠ABC=600,PA=AC=a,PB=PD= ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.
(1)证明PA⊥平面ABCD;
(2)求以AC为棱,EAC与DAC为面的二面角 的大小;
的大小;
 (3)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.
(3)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.
19.(本小题满分12分)
(理)已知函数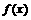 、
、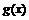 对任意实数
对任意实数 、
、 分别满足
分别满足
① 且
且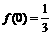 ;②
;② 且
且 ,
, 为正整数
为正整数
(1)求数列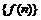 、
、 的通项公式;
的通项公式;
(2)设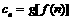 ,求数列
,求数列 的前
的前 项和.
项和.
(文)已知等比数列 ,
, ,
,
(1)求通项 ;
;
(2)若 ,数列
,数列 的前
的前 项的和为
项的和为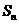 ,且
,且 ,求
,求 的值.
的值.
18.(本小题满分12分)
(理)某系统是由四个整流二极管(串、并)联结而成,已知每个二极管的可靠度为0.8
(即正常工作时),若要求系统的可靠度大于0.85,请你设计至少两种不同的联结方式,并说明理由.
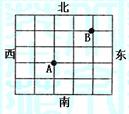 (文)如图是一个方格迷宫,甲、乙两人分别位于迷宫的A、B两处,现以每分钟一格的速度同时出发,在每个路口只能向东、西、南、北四个方向之一行走。若甲向东、向西行走的概率均为
(文)如图是一个方格迷宫,甲、乙两人分别位于迷宫的A、B两处,现以每分钟一格的速度同时出发,在每个路口只能向东、西、南、北四个方向之一行走。若甲向东、向西行走的概率均为 ,向南、向北行走的概率分别为
,向南、向北行走的概率分别为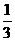 和p,乙向东、南、西、北四个方向行走的概率均为q
和p,乙向东、南、西、北四个方向行走的概率均为q
(1)求p和q的值;
(2)设至少经过t分钟,甲、乙两人能首次相遇,试确定t的值,并求t分钟时,甲
乙两人相遇的概率.
17.(本小题满分12分)设向量 =(cos23°,cos67°),
=(cos23°,cos67°), b=(cos68°,cos22°),
b=(cos68°,cos22°), (t∈R).
(t∈R).
(1)求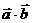 ;
;
(2)求 u的模的最小值.
u的模的最小值.
16.设函数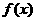 的定义域为
的定义域为 ,若存在常数
,若存在常数 ,使|
,使|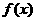 |≤
|≤ 对一切实数
对一切实数 均成立,则称
均成立,则称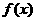 为
为 函数。给出下列函数:
函数。给出下列函数:
①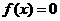 ;
;
② ;
;
③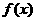 =
= ;
;
④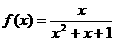 ;
;
⑤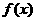 是R上的奇函数,且满足对一切实数
是R上的奇函数,且满足对一切实数 、
、 均有
均有 .
.
其中是 函数的序号为 。
函数的序号为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com