
题目列表(包括答案和解析)
32、给定一个圆锥和两个平面α、β,其中α∥β,且它们与圆锥底面平行,若平面α把圆锥侧面分成面积相等的两部分,平面β把圆锥分成体积相等的两部分,求夹在α、β间的几何体的体积与圆锥体积之比。
分析:本题涉及到截锥性质:截面积与底面积的比为对应元素的平方比,截得的圆锥的体积与原圆锥的体积之比是对应元素的立方比。
解:设给定圆锥的底面半径为R,高为H,则V圆锥=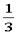 πR2H;
πR2H;
设平面α、β与圆锥侧面相交所得两圆半径分别为r1和r2,
由截锥性质得:
显然r2>r1,即平面β比平面α离圆锥底面近些,又设截得的两圆锥的高分别是h1和h2,则夹在α、β间的圆台的高h,有:
 h= h2-h1=
h= h2-h1=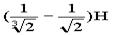 ;
;
V圆台=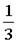 π×
π× ×(
×( )
)
=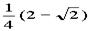 ×
× πR2H
πR2H
∴V圆台:V圆锥=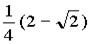
31、多面体表面积为S,外切于表面积为36π(平方单位)的球,求这个多面体的体积;
分析:可仿照平面几何类似问题,连结三角形的内切圆圆心和各个顶点的线段,将三角形面积分为三个部分,且有S=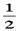 r(a+b+c);
r(a+b+c);
解:球的半径R=3,连结球心和多面体各个顶点
,得到的锥体体积之和就是多面体的体积,这些锥体的高都是半径R,故V=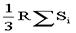 =S(立方单位)。
=S(立方单位)。
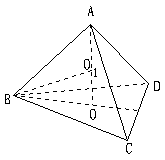
30、如图,四棱锥P-ABCD的侧棱PA⊥底面ABCD,底面ABCD是直角梯形,其中∠DAB=∠CBA=90°,又AD=AB=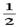 BC,∠APB=arcsin
BC,∠APB=arcsin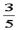 ,试求侧面APB与侧面CPD所成的角。
,试求侧面APB与侧面CPD所成的角。
 解:设AD=AB=
解:设AD=AB=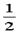 BC=3a,由Rt△PAB≌Rt△PAD,∠APB=arcsin
BC=3a,由Rt△PAB≌Rt△PAD,∠APB=arcsin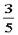 ,得PD=PB=5a,PA=4a,延长CD、BA交于E,连PE,作BF⊥PE于F,连CF,可证BC⊥平面PBE,则CF⊥PE( 三垂线定理),从而∠BFC是二面角B-PE-C的平面角,设其为θ; 显然AD是△EBC的中位线,∴EA=AB=3a,即EB=6a,可得PE=PB=5a
在△PBE中,用面积关系得:PE×BF=BE×PA
,得PD=PB=5a,PA=4a,延长CD、BA交于E,连PE,作BF⊥PE于F,连CF,可证BC⊥平面PBE,则CF⊥PE( 三垂线定理),从而∠BFC是二面角B-PE-C的平面角,设其为θ; 显然AD是△EBC的中位线,∴EA=AB=3a,即EB=6a,可得PE=PB=5a
在△PBE中,用面积关系得:PE×BF=BE×PA
∴BF=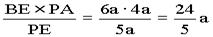 由Rt△BCF,
由Rt△BCF,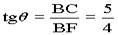 ,∴
,∴ ;
;
本题还可以用射影面积法。
29、三棱锥P-ABC中,三侧棱PA、PB、PC两两相互垂直,三侧面面积分别为S1、S2、S3,底面积为S,三侧面与底面分别成角α、β、γ,(1)求S(用S1、S2、S3表示);(2)求证:cos2α+cos2β+cos2γ=1;

 解:设PA=a,PB=b,PC=c,则S1=
解:设PA=a,PB=b,PC=c,则S1=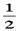 ab ,S2=
ab ,S2=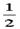 bc,S3=
bc,S3=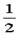 ca,
作PD⊥BC于D,连AD,易证BC⊥平面PAD,
ca,
作PD⊥BC于D,连AD,易证BC⊥平面PAD,
于是BC⊥AD;S△ABC= BC×AD,在Rt△APD中,AD2=a2+PD2,
在Rt△BPC中,PD2=
BC×AD,在Rt△APD中,AD2=a2+PD2,
在Rt△BPC中,PD2=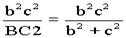 ,
∴AD2=a2+
,
∴AD2=a2+ ∴S△ABC2=(
∴S△ABC2=( BC×AD)2=
BC×AD)2=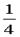 (a2b2+b2c2+c2a2)=
(a2b2+b2c2+c2a2)=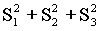 ∴
∴
证明:由(1)知,PD⊥BC,AD⊥BC,∴∠PDA是侧面PBC与底面ABC所成二面角的平面角,不妨设∠PDA=α,
PD2=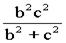 ,AD2=
,AD2=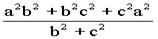 ∴cos2α=
∴cos2α=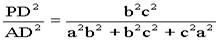 ;同理cos2β=
;同理cos2β=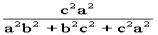 ;
cos2γ=
;
cos2γ=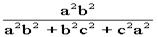 ;∴cos2α+cos2β+cos2γ=1
;∴cos2α+cos2β+cos2γ=1
28、过点S引三条长度相等不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,
∠BSC=90°,求证:平面ABC⊥平面BSC。
证明:作AO⊥平面SBC,O为垂足,
∵SA=SB,∠ASB=60°,∴AB=AS,同理AS=AC,∴AB=AS=AC,∴O为△BSC的外心,又∠BSC=90°,故O为BC中点,即AO在平面ABC内,所以平面ABC⊥平面BSC。
27、如图,四棱锥V-ABCD中,∠BCD=∠BAD=90°,
又∠BCV=∠BAV=90°,求证:VD⊥AC;
证明:∠BCD=∠BAD=90°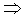 BC⊥CD,BA⊥AD
BC⊥CD,BA⊥AD
∠BCV=∠BAV=90°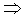 BC⊥CV,BA⊥AV,
BC⊥CV,BA⊥AV,
∴BC⊥平面VCD,BA⊥平面VAD ∴BC⊥VD,BA⊥VD
∴VD⊥平面ABC,∴VD⊥AC
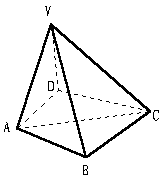
26、如图,正方体ABCD-A1B1C1D1的棱长为8cm,M、N、P分别是AB、A1D1、BB1的中点;(1)画出过M、N、P三点的平面与平面A1B1C1D1的交线以及与平面BB1C1C的交线;(2)设过M、N、P三点的平面与B1C1交于点Q,求PQ的长;
解:(1)设M、N、P三点确定的平面为α,则α与平面AA1B1B的交线为直线MP,设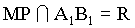 ,则RN是α与平面A1B1C1D1的交线,设
,则RN是α与平面A1B1C1D1的交线,设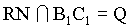 ,则直线PQ就是所要画的平面α与平面BB1C1C的交线;
,则直线PQ就是所要画的平面α与平面BB1C1C的交线;

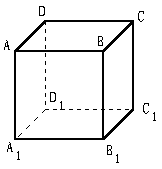
(2)正方体的棱长为8cm,B1R=BM=4cm,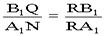 ,
,
故B1Q= 4=
4=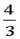 (cm),在Rt△PB1Q中,B1P=4cm,B1Q=
(cm),在Rt△PB1Q中,B1P=4cm,B1Q= cm,
cm,
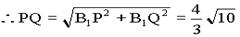 (cm)
(cm)
25、如图:已知平面四边形ABCD,AC、BD相交于O,AB=AD,CB=CD,
∠ABC=120°,且PA⊥平面ABCD.
(1)若AB=PA=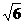 ,求P到直线BC的距离;
,求P到直线BC的距离;
(2)求证平面PBD⊥平面PAC.
证明(1)延长CB,过A在平面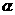 内作AE⊥CB,垂足为E.
内作AE⊥CB,垂足为E.
∵∠ABC=120°,∴∠ABE=60°,在Rt△ABE中:AE=AB·sin60°=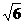 ·
·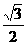 =
=
∵PA⊥平面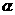 ,AE⊥EB,∴AE是PE在平面
,AE⊥EB,∴AE是PE在平面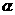 内的射影,
内的射影,
∴PE⊥EB,∴PE为点P到BC的距离.在Rt△PAE中:
 PE=
PE= .
.
(2)在四边形ABCD中,取BD中点O,连AO、CO,
∵AB=AD,CD=CB,BO=OD,
∴AO⊥BD,CO⊥BD, ∴A、O、C共线,∴AC⊥BD.
又PA⊥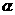 ,∴PA⊥BD,
,∴PA⊥BD,
∴BD⊥平面PAC,∵BD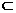 平面PBD, ∴平面PBD⊥平面PAC.
平面PBD, ∴平面PBD⊥平面PAC.
23、 在三棱锥A-BCD中,E、F分别是线段AD、BC上的点,满足
在三棱锥A-BCD中,E、F分别是线段AD、BC上的点,满足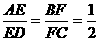 ,AB=CD=3,且AB与CD所成的角为60o,求EF的长.
,AB=CD=3,且AB与CD所成的角为60o,求EF的长.
解:如图,过E 分别作EG∥AB
交BD于G,EH∥DC交AC于H,
连接GH、FH,由条件,易知
EGFH为平行四边形。
∴∠GEH为异面直线AB与CD
所成的角或其补角。∴∠GEH=60°或120°
又EG=AB=2,EH=AB=1,
由余弦定理得:EF== 或
或
翰林汇24、如图,△ABC和△DBC所在平面互相垂直 ,AB=BC=BD,∠CBA=∠DBC=120o,求
(1) AD与平面BCD的成角;
(2) AD与BC的成角;
(3) 二面角A-BD-C的正切值.
解:(1)如图,过A作AE⊥CB与CB的延长线交与E,连接DE,
∵平面ABC⊥平面DBC∴AE⊥平面DBC,
 ∴∠ADE即为AD与平面CBD所成的角。
∴∠ADE即为AD与平面CBD所成的角。
∵AB=BD,∠CBA=∠DBC,EB=EB
∴∠ABE=∠DBE,∴△DBE≌△ABE
∴DE⊥CB且DE=AE
∴∠ADB=45°∴AD与平面CBD
所成的角为45°
(2)由(1)知CB⊥平面ADE
∴AD⊥BC即AD与BC所成的角为90°.
(3)过E作EM⊥BD于M
由(2)及三垂线定理知,AM⊥BD,
∴∠AME为二面角A-BD-C的平面角的补角.
∵AE=BE=2ME,∴tg∠AME=2,故二面角A-BD-C的正切值为-2.
22、
 矩形ABCD(AB≤BC)中,AC=2
矩形ABCD(AB≤BC)中,AC=2 ,沿对角线AC把它折成直二面角B-AC-D后,BD=
,沿对角线AC把它折成直二面角B-AC-D后,BD=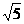 ,求AB、BC的长.
,求AB、BC的长.
翰林汇
翰林汇解:如图,
分别过B、D作BE⊥AC于E,DF⊥AC于F,
设∠BAC=θ,则AB=ACcosθ=2cosθ,
BE=DE=ABsinθ=sin2θ,
AE=ABcosθ=2cos2θ∴EF=AC-2AE
=2=-2cos2θ
折叠后,在平面ACD内过E作EG∥FD,且EG=FD,连接DG、BG、BD,则∠BEG为二面角B-AC-D的平面角,∴∠BEG=90°
于是BG=BE=sin2θ=2sin2θ
∴BG2+DG2=BD2,即:(2sin2θ)2+(-2cos2θ)2=5
∴4(cos2θ)2=1,∴cos2θ=±,
∵AB≤BC,∴cos2θ=-∴cosθ=,故AB= ,BC=
,BC=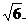
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com