
题目列表(包括答案和解析)
9.若x、y∈R,且2x-1+i=y-(3-y)i,则x=__________,y=___________.
解析:根据复数相等的定义求得.
答案: 4
4
8.复数z= |-2i的模为_______________.
|-2i的模为_______________.
解析:由复数的模的性质可知
z= -2i
-2i
= -2i=
-2i= -2i,∴|z|=3.
-2i,∴|z|=3.
答案:3
7.已知M={1,2,(a2-3a-1)+(a2-5a-6)i},N={-1,3},M∩N={3},实数a=_________.
解析:按题意(a2-3a-1)+(a2-5a-6)i=3,
∴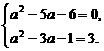 解得a=-1.
解得a=-1.
答案:-1
6.已知复数(x-2)+yi(x、y∈R)的模为 ,则
,则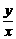 的最大值是
的最大值是
A. B.
B. C.
C. D.
D.
解析:∵|x-2+yi|= ,
,
∴(x-2)2+y2=3.

∴(x,y)在以C(2,0)为圆心、以 为半径的圆上,如右图,由平面几何知识知
为半径的圆上,如右图,由平面几何知识知 .
.
答案:D
5.已知复平面内的圆M:|z-2|=1,若 为纯虚数,则与复数p对应的点P
为纯虚数,则与复数p对应的点P
A.必在圆M上 B.必在圆M内
C.必在圆M外 D.不能确定
解析:∵ 为纯虚数,设为ki(k∈R,k≠0),
为纯虚数,设为ki(k∈R,k≠0),
∴(1-ki)p=1+ki,取模得|p|=1且p≠1.
∴选C.
答案:C
4.设f(n)=( )n+(
)n+( )n(n∈Z),则集合{x|x=f(n)}中元素的个数是
)n(n∈Z),则集合{x|x=f(n)}中元素的个数是
A.1 B.2 C.3 D.无穷多个
解析:∵f(n)=in+(-i)n,
∴f(0)=2,f(1)=i-i=0,f(2)=-1-1=-2,f(3)=-i+i=0.
∴{x|x=f(n)}={-2,0,2}.
答案:C
3.在下列命题中,正确命题的个数为
①两个复数不能比较大小;
②z1、z2、z3∈C,若(z1-z2)2+(z2-z3)2=0,则z1=z3;
③若(x2-1)+(x2+3x+2)i是纯虚数,则实数x=±1;
④z为虚数的一个充要条件是z+ ∈R;
∈R;
⑤若a、b是两个相等的实数,则(a-b)+(a+b)i是纯虚数;
⑥复数z∈R的一个充要条件是z= .
.
A.0 B.1 C.2 D.3
解析:①错,两个复数如果都是实数则可比较大小;②错,当z1、z2、z3不全是实数时不成立,如z1=i,z2=1+i,z3=1时满足条件,但z1≠z3;③错,当x=-1时,虚部也为零,原数是实数;④错,此条件是必要非充分条件;⑤错,当a=b=0时,原数是实数;⑥对.
答案:B
2.当 <m<1时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于
<m<1时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:z对应的点为(3m-2,m-1),
∵ <m<1,
<m<1,
∴0<3m-2<1,- <m-1<0.
<m-1<0.
答案:D
1.如果复数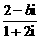 (其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
(其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
A.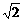 B.
B. C.-
C.- D.2
D.2
解析: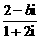 =
= =
=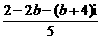
∴2-2b=b+4,b=- .
.
答案:C
22.有点难度哟!
(14分)某数学家随身带着甲、乙两盒火柴,每盒有n根,每次用时,随机地任取一盒,然后从中抽取一根(巴拿赫火柴问题).求:
(1)第一次发现一盒空时,另一盒恰剩r根火柴的概率(r=0,1,…,n);
(2)第一次用完一盒火柴(不是发现空)时另一盒恰剩r根火柴的概率(r=1,2,…,n).
分析:第n+1次取到甲盒时,才发现甲盒空,但第n次取甲盒后即已用完甲盒火柴.因此(1)(2)中的两个事件不同.
解:(1)记A=“首次发现一盒空时另一盒恰剩r根火柴”,
B=“首次发现的空盒是甲盒且此时乙盒恰剩r根火柴”,
C=“首次发现的空盒是乙盒且此时甲盒恰剩r根火柴”.
则事件B与C互斥,A=B+C.
由于甲、乙盒所处地位相同,故P(B)=P(C).
为求P(B),令D=“在甲、乙两盒中任取一盒,得到甲盒”,则P(D)=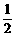 .
.
事件B发生相当于独立重复地做了2n-r+1次试验,前2n-r次D恰好发生n次、第2n-r+1次D也发生.
因此P(B)=C (
(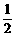 )n(1-
)n(1-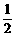 )n-r·
)n-r·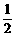
= C
C ,
,
P(A)=P(B)+P(C)=2P(B)= C
C .
.
(2)记E=“首次用完一盒时另一盒恰有r根”,
F(G)=“首次用完的是甲(乙)盒且此时乙(甲)盒恰有r根火柴”.
则事件F与G互斥,E=F+G.
事件F发生相当于独立重复地做了2n-r次试验,前2n-r-1次D恰好发生n-1次,第2n-r次D也发生.
故P(F)=C (
(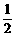 )n-1(1-
)n-1(1-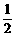 )n-r·
)n-r·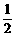 =
= C
C .
.
类似(1),P(E)=P(F)+P(G)=2P(F)= C
C .
.
评述:改记A为Ar,则A0,A1,…,An彼此互斥,和是必然事件,故
 C
C =1;
=1;
改记E为Er,则E1,E2,…,En也彼此互斥,和是必然事件,
故
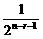 C
C =1.
=1.
因此使用概率方法我们可以得到一些恒等式.
(1)中分别取r=0和n,得
P(首次发现一盒空时另一盒也空)=C
 ,
,
P(首次发现一盒空时另一盒原封未动)= ;
;
(2)中取r=n,得
P(用完一盒时另一盒原封未动)= .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com