3、函数g(x)=x²，若a≠0且a∈R, 则下列点一定在函数y=g(x)的图象上的是( 　)。

　 (A)(-a, -g(-a)) (B)(a, g(-a)) (C)(a, -g(a)) (D)(-a, -g(a))

　 提示：本题从函数的奇偶性入手。

2、函数y=f (x)是R上的增函数，则a+b>0是f (a)+f (b)>f (-a)+f (-b)的(　 )条件。

　 (A)充分不必要　 (B)必要不充分　 (C)充要　 　　　(D)不充分不必要

提示：由a>-b 以及 y = f ( x )在R上为增函数可知：f ( a )　 > f ( b ) ，f ( b )　 > f ( - a )，反过来，由增函数的概念也可推出，a+b>(-a)+(-b)。

1、同时满足① M{1, 2, 3, 4, 5}; ② 若a∈M，则(6-a)∈M, 的非空集合M有(　 )。

　 (A)16个　 (B)15个　 (C)7个　 (D)8个

　 提示：着重理解“∈”的意义，对M中元素的情况进行讨论，分别讨论“一个、两个、三个、四个、五个元素”等几种情况，得出相应结论。

11.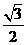,　　　 12.　 3/4　 13. 7/2(或3.5 )　　　 14. -1；

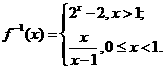
20．(本小题满分14分) 已知数列{a_n}满足：(n∈N^*)，a₁∈(0，1)．

(1)求证：当n>1时，；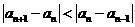

(2)是否存在常数λ，使得对任何大于2的n，不等式都成立？如果存在，请求出一个这样的λ值；如果不存在，请说明理由．

一模答案

BADCD　 DBCAC

19．(本小题满分14分) 　已知平面内一个定点A(1,0)和定直线l:x=-1，P是平面内一个动点，PM⊥l，垂足为M，．

(1)求点P的轨迹方程；

(2)过A作直线QR与P的轨迹交于Q、R两点，求三角形OQR面积的最小值(O为坐标原点)．

18．(本小题满分14分)某投资人打算作投资，有两个项目在考虑的范围内．据评估，甲、乙两个项目盈利的可能性分别为70%和50%，盈利率分别是40%和50%，亏损的可能性分别是15%和20%，其相应的亏损率分别为20%和15%，其余的情况是不盈不亏．投资人计划投资金额不超过20万元．

1)如果投资人在甲、乙两个项目分别投资10万元，问期望盈利是多少万元？

2)如果投资人要求确保期望盈利在4．82万元以上，问投资人对甲、乙两个项目分别投资多少万元，才能保证在两个项目都亏损的情况下，亏损额最小？

17．(本小题满分14分) 如图，直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，A₁B₁=2，A₁C₁=1，D为棱CC₁中点，AB₁⊥BD．

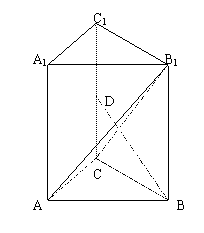1)求证：B₁C⊥BD；

2)求直三棱柱体积V．

16．(本小题满分12分)

解关于x的不等式：(0≤a＜4)

15．(本小题满分12分) 已知在△ABC中, 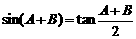,且三边a,b,c成等差数列,求三角形内切圆与外接圆的面积之比.