
题目列表(包括答案和解析)
11. :如图,设OA、OB是过抛物线y2=2px顶点O的两条弦,且=0,求以OA、OB为直径的两圆的另一个交点P的轨迹.(13分)
10. 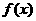 对任意
对任意 都有
都有
(Ⅰ)求 和
和 的值.
的值.
(Ⅱ)数列 满足:
满足: =
= +
+ ,数列
,数列 是等差数列吗?请给予证明;
是等差数列吗?请给予证明;
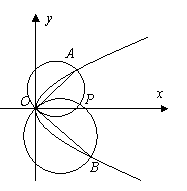 (Ⅲ)令
(Ⅲ)令
试比较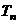 与
与 的大小.
的大小.
9.已知焦点在 轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点
轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点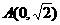 为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线 对称.
对称.
(Ⅰ)求双曲线C的方程;
(Ⅱ)设直线 与双曲线C的左支交于A,B两点,另一直线
与双曲线C的左支交于A,B两点,另一直线 经过M(-2,0)及AB的中点,求直线
经过M(-2,0)及AB的中点,求直线 在
在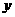 轴上的截距b的取值范围;
轴上的截距b的取值范围;
(Ⅲ)若Q是双曲线C上的任一点, 为双曲线C的左,右两个焦点,从
为双曲线C的左,右两个焦点,从 引
引 的平分线的垂线,垂足为N,试求点N的轨迹方程.
的平分线的垂线,垂足为N,试求点N的轨迹方程.
8.已知数列{an}满足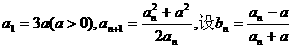
(1)求数列{bn}的通项公式;
(2)设数列{bn}的前项和为Sn,试比较Sn与 的大小,并证明你的结论.
的大小,并证明你的结论.
4.以椭圆 =1(a>1)短轴一端点为直角顶点,作椭圆内接等腰直角三角形,试判断并推证能作出多少个符合条件的三角形.
=1(a>1)短轴一端点为直角顶点,作椭圆内接等腰直角三角形,试判断并推证能作出多少个符合条件的三角形.
5 已知,二次函数f(x)=ax2+bx+c及一次函数g(x)=-bx,其中a、b、c∈R,a>b>c,a+b+c=0.
(Ⅰ)求证:f(x)及g(x)两函数图象相交于相异两点;
(Ⅱ)设f(x)、g(x)两图象交于A、B两点,当AB线段在x轴上射影为A1B1时,试求|A1B1|的取值范围.
6
已知过函数f(x)= 的图象上一点B(1,b)的切线的斜率为-3。
的图象上一点B(1,b)的切线的斜率为-3。
(1) 求a、b的值;
(2) 求A的取值范围,使不等式f(x)≤A-1987对于x∈[-1,4]恒成立;
(3)
令 。是否存在一个实数t,使得当
。是否存在一个实数t,使得当 时,g(x)有最大值1?
时,g(x)有最大值1?
7
已知两点M(-2,0),N(2,0),动点P在y轴上的射影为H,︱ ︱是2和
︱是2和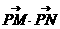 的等比中项。
的等比中项。
(1) 求动点P的轨迹方程,并指出方程所表示的曲线;
(2) 若以点M、N为焦点的双曲线C过直线x+y=1上的点Q,求实轴最长的双曲线C的方程。
3.(本题满分12分)如图,已知点F(0,1),直线L:y=-2,及圆C: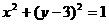 。
。
(1) 若动点M到点F的距离比它到直线L的距离小1,求动点M的轨迹E的方程;
(2) 过点F的直线g交轨迹E于G(x1,y1)、H(x2,y2)两点,求证:x1x2 为定值;
(3) 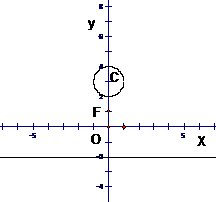 过轨迹E上一点P作圆C的切线,切点为A、B,要使四边形PACB的面积S最小,求点P的坐标及S的最小值。
过轨迹E上一点P作圆C的切线,切点为A、B,要使四边形PACB的面积S最小,求点P的坐标及S的最小值。
2.
已知函数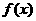 对任意实数x都有
对任意实数x都有 ,且当
,且当 时,
时, 。
。
(1)  时,求
时,求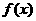 的表达式。
的表达式。
(2) 证明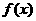 是偶函数。
是偶函数。
(3) 试问方程 是否有实数根?若有实数根,指出实数根的个数;若没有实数根,请说明理由。当
是否有实数根?若有实数根,指出实数根的个数;若没有实数根,请说明理由。当
1.椭圆的中心是原点O,它的短轴长为 ,相应于焦点
,相应于焦点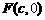 (
( )的准线
)的准线 与x轴相交于点
与x轴相交于点 ,
, ,过点
,过点 的直线与椭圆相交于
的直线与椭圆相交于 、
、 两点。
两点。
(1)求椭圆的方程及离心率;
(2)若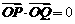 ,求直线
,求直线 的方程;
的方程;
(3)设 (
(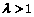 ),过点
),过点 且平行于准线
且平行于准线 的直线与椭圆相交于另一点
的直线与椭圆相交于另一点 ,证明
,证明 . (14分)
. (14分)
例6.(04年黄冈.秋调研9)把正整数按下图所示的规律排序,则从2003到2005的箭头方向依次为( B ).

练10.(05年湛江市.1月质检14)某住宅小区有居民2万户,从中随机抽取200户,调查是否安装宽带,调查结果如下表所示:
|
宽带 |
动迁户 |
原住户 |
|
已安装 |
60 |
35 |
|
未安装 |
45 |
60 |
则该小区已安装宽带的户数估计有 户.
例5.(05年江苏.15市模拟15)“渐减数”是指每个数字比其左边数字小的正整数(如98765),若把所有五位渐减数按从小到大的顺序排列,则第55个数为 .
练9.(05年朝阳区.1月质检13)将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱的两端异色,若只有五种颜色可供使用,则不同的染色方法总数为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com