
题目列表(包括答案和解析)
28. (1) ∵函数f(x)= 的图象过原点,即f(0)=0,∴c =0,∴f(x)= .
又函数f(x)= = b - 的图象关于点(-1,1)成中心对称,∴a=1,b=1,∴f(x)= .(2)由题意有an+1=[ ]2,即 = ,即 = +1,∴ - =1.
∴数列{}是以1为首项,1为公差的等差数列. ∴ =1+(n-1)=n,即 = ,∴an= .∴a2= ,a3= ,a4= ,an= .
27.解(理)(1)易得l的方程为 …1分 由
…1分 由 ,得(a2t2+4)y2-4aty=0…2分
,得(a2t2+4)y2-4aty=0…2分
解得y=0或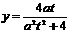 即点M的纵坐标
即点M的纵坐标 ………………4分
………………4分
S=S△AMN=2S△AOM=|OA|·yM=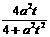 …7分 (2)由(1)得,
…7分 (2)由(1)得,
令 …………9分 由
…………9分 由
当 时,
时,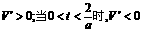 …10分 若1≤a≤2,则
…10分 若1≤a≤2,则 ,故当
,故当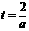 时,Smax=a11分
时,Smax=a11分
若a>2,则 在[1,2]上递增,进而S(t)为减函数. ∴当t=1时,
在[1,2]上递增,进而S(t)为减函数. ∴当t=1时, 13分
13分
综上可得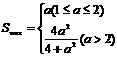 …………14分
…………14分
26、解:⑴设E(x,y),D(x0,y0)
∵ABCD是平行四边形,∴ ,
,
∴(4,0)+(x0+2,y0)=2(x+2,y)∴(x0+6,y0)=(2x+4,2y)
∴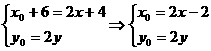
又
即: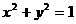
∴□ABCD对角线交点E的轨迹方程为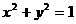
⑵设过A的直线方程为
以A、B为焦点的椭圆的焦距2C=4,则C=2
设椭圆方程为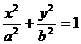 , 即
, 即 …………………(*)
…………………(*)
将 代入(*)得
代入(*)得 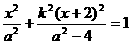
即 
设M(x1,y1),N(x2,y2)则
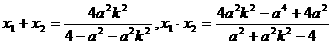
∵MN中点到Y轴的距离为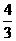 ,且MN过点A,而点A在Y轴的左侧,∴MN中点也在Y轴的左侧。
,且MN过点A,而点A在Y轴的左侧,∴MN中点也在Y轴的左侧。
∴ ,∴
,∴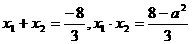
∴
∵ ∴
∴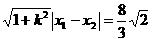
∴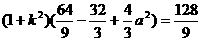 即
即 
∴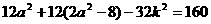 ∴
∴
∴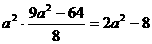 ,
, 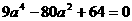
 ,∵
,∵ ,∴
,∴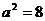
∴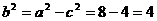
∴所求椭圆方程为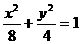
⑶由⑴可知点E的轨迹是圆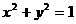
设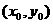 是圆上的任一点,则过
是圆上的任一点,则过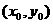 点的切线方程是
点的切线方程是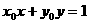
①当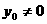 时,
时,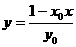 代入椭圆方程得:
代入椭圆方程得:
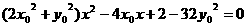 ,又
,又
∴

∴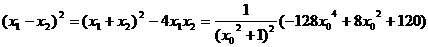

=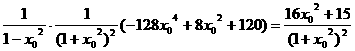
令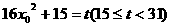
则 , ∵
, ∵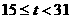
∴当t=15时,  取最大值为15 ,
取最大值为15 ,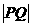 的最大值为
的最大值为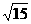 。
。
此时  ,∴直线l的方程为
,∴直线l的方程为
②当 时,容易求得
时,容易求得
故:所求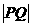 的最大值为
的最大值为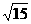 ,此时l的方程为
,此时l的方程为
25、解:⑴由题意易得M(-1,0)
设过点M的直线方程为 代入
代入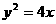 得
得
 ………………………………………(1)
………………………………………(1)
再设A(x1,y1),B(x2,y2)
则x1+x2= ,x1·x2=1
,x1·x2=1
y1+y2=k(x1+1)+k(x2+1)=k(x1+x2)+2k=
∴AB的中点坐标为( )
)
那么线段AB的垂直平分线方程为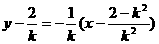 ,令
,令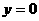 得
得
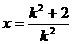 ,即
,即
又方程(1)中△=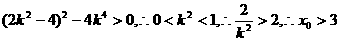
⑵若△ABD是正三角形,则需点D到AB的距离等于
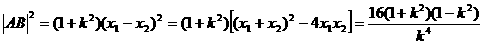
点到AB的距离d=
据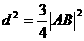 得:
得:
∴ ,∴
,∴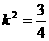 ,满足
,满足
∴△ABD可以为正△,此时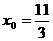
24、(1)当X<0时, 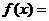
 (3分)
(3分)
(2)函数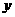 =
=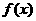 (X
(X 0)在
0)在 是增函数;(证明略)
(9分)
是增函数;(证明略)
(9分)
(3)因为函数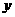 =
=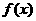 (X
(X 0)在
0)在 是增函数,由x
是增函数,由x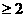 得
得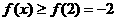 ;
;
又因为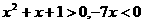 ,所以
,所以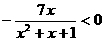 ,所以
,所以 ;
;
因为 ,所以
,所以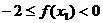 ,且
,且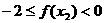 ,即
,即 ,
,
所以,-2≤f(x1)
– f(x2) ≤2即|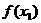 -
- |<2. (14分)
|<2. (14分)
23、(1)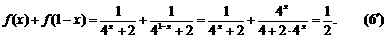

22、解析:(1)如图,以AB所在直线为x轴,AB中垂线为y轴建立直角坐标系,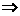 A(-1,0),B(1,0)
A(-1,0),B(1,0)

设椭圆方程为:
令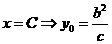 ∴
∴
∴ 椭圆C的方程是: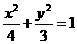
(2) ,
,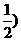 ,l⊥AB时不符,
,l⊥AB时不符,
设l:y=kx+m(k≠0)
由 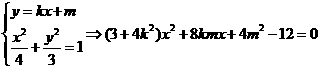
M、N存在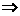
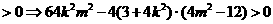
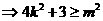
设M( ,
,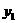 ),N(
),N(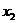 ,
,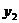 ),MN的中点F(
),MN的中点F( ,
, )
)
∴ 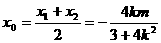 ,
,

∴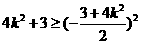 ∴
∴ ∴
∴ ∴
∴ 且
且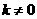
∴ l与AB的夹角的范围是 ,
, .
.
21、解:(1)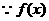 为偶函数
为偶函数 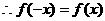

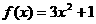
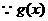 为奇函数
为奇函数 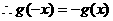



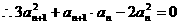


 是以
是以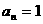 为首项,公比为
为首项,公比为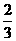 的等比数列.
的等比数列. 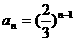
(2)

20.(1)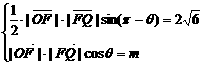
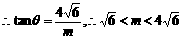


(2)设所求的双曲线方程为
 又由
又由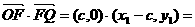
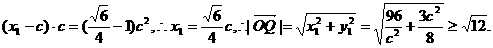
当且仅当c=4时,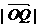 最小,此时Q的坐标为
最小,此时Q的坐标为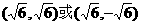
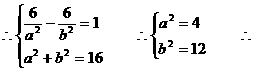 所求方程为
所求方程为
(3)设
 的方程为
的方程为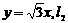 的方程为
的方程为 则有
则有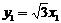 ①
①
 ②
② 
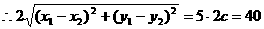
 ③ 设
③ 设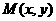 由①②得
由①②得

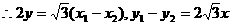
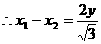 ,
,
 代入③得
代入③得
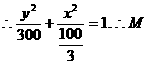 的轨迹为
的轨迹为
焦点在y轴上的椭圆.
19.(1)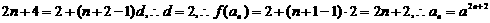
(2)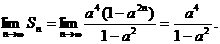
(3)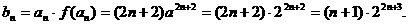

 为递增数列
为递增数列 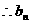 中最小项为
中最小项为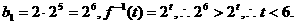
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com