
题目列表(包括答案和解析)
14、14.函数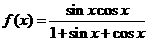 的值域为______________。
的值域为______________。
13、已知 为实数,
为实数, 展开式中
展开式中 的系数为
的系数为 ,则
,则 .
.
12、如果正△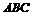 中,
中, ,向量
,向量 ,那么以
,那么以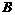 ,
,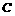 为焦点且过点
为焦点且过点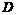 ,
, 的双曲线的离心率是
.
的双曲线的离心率是
.
11、将棱长为1的正方体木块加工成一个体积最大的球,则这个球的体积为 ,
球的表面积为 (不计损耗).
(13)设函数f(x)=logax(a>0且a≠1)满足f(9)=2,则f-1(log92)= .
(14)点M在抛物线y2=ax上运动,点N与点M关于点A(1,1)对称,则点N的轨迹方程是 .
(15)有5列客车停在某车站并行的5条火车轨道上,若快车A不能停在第3道上,慢车B
不能停在第1道上,则5列客车的停车方法共有 种(用数字作答).
(16)已知数列{an}的通项an=(2n+1)·2n-1,前n项和为Sn,则Sn= .
三、解答题(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤)
(17)(本小题满分10分)
已知0°<x<45°,且 .
.
求cos
(18)(本小题满分12分)
已知:在等差数列{an}中,a1=1,d≠0,若Sn=a1+a2+……an,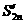 =an+1+an+2+……+a3n,且Sn与
=an+1+an+2+……+a3n,且Sn与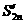 的比与n无关.
的比与n无关.
(Ⅰ)求等差数列{an}的通项公式;
(Ⅱ)求 的值.
的值.
(19)(本小题满分12分)
如图,已知直三棱柱ABC-A1B1C1中,AB=AC,D为BC中点,F为BB1上一点,
 BF=BC=2,FB1=1.
BF=BC=2,FB1=1.
(Ⅰ)求证AD⊥平面BB1C1C;
(Ⅱ)若E为AD上不同于A、D的任一点,求证:EF⊥FC1;
(Ⅲ)若A1B1=3,求FC1与平面AA1B1B所成角的大小.
(20)(本小题满分12分)
某房地产公司要在荒地ABCDE(如图)上划出一块长方形地面(不改变方向)建造一幢8层楼公寓,问如何设计才能使公寓占地面积最大,并求出最大面积(精确到1m2).

(21)(本小题满分14分)
如图,椭圆的中心在原点,长轴AA1在x轴上.以A、A1为焦点的双曲线交椭圆于C、D、D1、C1四点,且|CD|= |AA1|.椭圆的一条弦AC交双曲线于E,设
|AA1|.椭圆的一条弦AC交双曲线于E,设 ,当
,当 时,求双曲线的离心率e的取值范围.
时,求双曲线的离心率e的取值范围.

(22)(本小题满分14分
已知二次函数 设方程f(x)=x有两个实数根x1、x2.
设方程f(x)=x有两个实数根x1、x2.
(Ⅰ)如果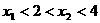 ,设函数f(x)的对称轴为x=x0,求证x0>-1;
,设函数f(x)的对称轴为x=x0,求证x0>-1;
(Ⅱ)如果 ,且f(x)=x的两实根相差为2,求实数b
的取值范围.
,且f(x)=x的两实根相差为2,求实数b
的取值范围.
(1)已知全集I,M、N是I的非空子集,若 ,则必有 (
)
,则必有 (
)
(A) (B)
(B) (C)
(C) (D)
(D)
 (2)在棱长为4的正方体ABCD-A1B1C1D1中,P是A1B1上一点,且
(2)在棱长为4的正方体ABCD-A1B1C1D1中,P是A1B1上一点,且 ,则多面体BC-PB1C1的体积为 ( )
,则多面体BC-PB1C1的体积为 ( )
(A) (B)
(B)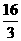
(C)4 (D)16
(3)已知直线 与
与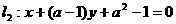 平行,则实数a的取值是
平行,则实数a的取值是
( )
(A)-1或2 (B)0或1 (C)-1 (D)2
(4)设 、A为正常数,
、A为正常数, ( )
( )
(A)充要条件 (B)充分不必要条件
(C)必要不充分条件 (D)既不充分又不必要条件
(5)已知 ,则a、b、c的大小顺序
,则a、b、c的大小顺序
是 ( )
(A)a>b>c (B)c>a>b (C)b>a>c (D)b>c>a
(6)复数z满足条件 则z的值为 (
)
则z的值为 (
)
(A)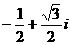 (B)
(B)
(C) (D)
(D)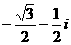
(7)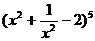 展开式的常数项是 (
)
展开式的常数项是 (
)
(A)252 (B)-252 (C)210 (D)-210
(8)已知下列命题:
①若直线a∥平面α,直线 ,则a∥b;
,则a∥b;
②若直线a∥平面α, 平面β,
平面β, ,a在α内的射影为a′,则a′∥b;
,a在α内的射影为a′,则a′∥b;
③若直线a⊥直线c,直线b⊥直线c,则直线a∥直线b;
④若α、β、γ、δ是不同的平面,且满足 ∥
∥
δ,其中正确命题的序号是 ( )
(A)①③ (B)②④ (C)② (D)④
(9)设△ABC的三边长a、b、c满足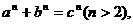 则△ABC是 ( )
则△ABC是 ( )
(A)钝角三角形 (B)锐角三角形 (C)等腰直角三角形 (D)非等腰的直角三角形
(10)直线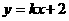 与椭圆
与椭圆 交于A、B两点,O是坐标原点,当直线OA、
交于A、B两点,O是坐标原点,当直线OA、
OB的斜率之和为3时,直线AB的方程是 ( )
 (A)2x-ey-4=0 (B)2x+3y-4=0 (C)3x+2y-4=0 (D)3x-2y-4=0
(A)2x-ey-4=0 (B)2x+3y-4=0 (C)3x+2y-4=0 (D)3x-2y-4=0
(11)如图,△ABC是Rt△AB为斜边,三个顶点A、B、C在平面α内的射影分别是A1、B1、C1.如果△A1B1C1是等边三角形,且AA1=m,BB1=m+2,CC1=m+1,并设平面ABC与平面A1B1C1所成的二面角的平面角为 则
则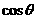 的值为 (
)
的值为 (
)
(A) (B)
(B) (C)
(C) (D)
(D)
 (12)如图,半径为2的⊙○切直线MN于点P,射线PK从PN出发绕点P逆时针方向旋转到PM,旋转过程中,PK交⊙○于点Q,设∠POQ为x,弓形PmQ的面积为S=f(x),那么f(x)的图象大致是
(12)如图,半径为2的⊙○切直线MN于点P,射线PK从PN出发绕点P逆时针方向旋转到PM,旋转过程中,PK交⊙○于点Q,设∠POQ为x,弓形PmQ的面积为S=f(x),那么f(x)的图象大致是




第Ⅱ卷(非选择题 共60分)
22.(本小题满分12分)
以一年为一个周期调查某商品出厂价格及该商品在商店销售价格时发现:该商品的出厂价格是在6元基础上按月份随正弦曲线波动的,已知3月份出厂价格最高为8元,7月份出厂价格最低为4元;而该商品在商店内的销售价格是在8元基础上按月份也是随正弦曲线波动的,并已知5月份销售价最高为10元,9月份销售价最低为6元.假设某商店每月购进这种商品m件,且当月能售完,请估计哪个月盈利最大?并说明理由.
21.(本小题满分12分)
椭圆的中心在坐标原点O,右焦点F(c,0)到相应准线的距离为1,倾斜角为45°的直线交椭圆于A,B两点.设AB中点为M,直线AB与OM的夹角为 a.
a.
(1)用半焦距c表示椭圆的方程及tg ;
;
(2)若2<tg <3,求椭圆率心率e的取值范围.
<3,求椭圆率心率e的取值范围.
20.(本小题满分12分)
已知函数
(1)当m=1时,解不等式
(2)如果对满足|m|<1的一切实数m,都有f(x)>g(x)求x的取值范围.
19.(本小题满分14分)
已知等差数列{an}的前四项和为60,第二项与第四项和为34;等比数列{bn}的前四项和为120,第二项与第四项和为90.
(1)求数列{an},{bn}的通项公式;
(2)是否存在正整数p.使得ap=b2 n对一切n∈N均成立?若存在请给出证明;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com