
题目列表(包括答案和解析)
10. 解析: 曲线是右半单位圆和下半单位圆的并集,右半单位圆方程是x- =0(x≥0);下半单位圆方程是y+
=0(x≥0);下半单位圆方程是y+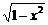 =0(y≤0). 答案:
D
=0(y≤0). 答案:
D
9. 解析: 设正方形ABCD的边为长1,则AC=2c=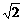 ,c=
,c= ,2a=|PA|+|PC|=
,2a=|PA|+|PC|= +
+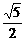 , a=
, a= +
+
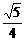 ,∴e=
,∴e= =
= (
(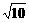 -
-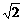 ).答案: C
).答案: C
8.解析: 由已知可得f(x1)+f(x2)+…+f(x2005)=8,
又f(x12)+f(x22)+…+f(x20052)
=2[f(x1)+f(x2)+…+f(x2005)]
=2×8=16. 答案: C
7.解析: 依定义:f(x)=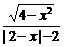
 |x|≤2且x≠0,∴f(x)=-
|x|≤2且x≠0,∴f(x)=- 为奇函数. 答案:
A
为奇函数. 答案:
A
6.解析:
解法一:设A、B、C分别表示“甲被录取”“乙被录取”“丙被录取”三个命题.则判断①为非A B且C;判断②为非B或非C为真;判断③为非A或B为真.
B且C;判断②为非B或非C为真;判断③为非A或B为真.
①的逆否命题为非B或非C A,结合②可知A为真,即甲被录取.由A真可知非A为假,结合③可知B为真,即乙被录取.
A,结合②可知A为真,即甲被录取.由A真可知非A为假,结合③可知B为真,即乙被录取.
解法二:根据判断①.若甲未被录取,则乙与丙都被录取,这与②矛盾.故甲被录取.由于③正确,故“甲未被录取”与“乙被录取”中至少一个正确.由于“甲未被录取”不正确,故“乙被录取”正确. 答案: D
5.解析: 易知x2+ax+b含x-2的因式,可设x2+ax+b=(x-2)(x+c),则原式
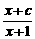 =2,即
=2,即 =2,∴c=4
=2,∴c=4 x2+ax+b=(x-2)(x+4)
x2+ax+b=(x-2)(x+4) a=2,b=-8. 答案:
C
a=2,b=-8. 答案:
C
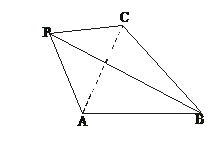
4.解析: 作PO⊥面ABC,O为垂足,连结OB交AC于D.连结PD,
∵PB⊥AC,∴AC⊥BD.
∴AC⊥面PDB.
∴AC⊥PD.
∴∠PDB为侧面PAC与底面ABC所成的二面角.
∴∠PDB=120°,∠PDO=60°.
∵△ABC为边长是2的正三角形,
∴AD=1.
又PA=3,
∴PD= =
=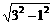 =2
=2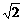 .
.
在△POD中,PO=PDsin60°=2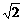 ×
× =
= . 答案: A
. 答案: A
3.  解析: ∵直线ax+by+c=0与圆x2+y2=1相离,∴
解析: ∵直线ax+by+c=0与圆x2+y2=1相离,∴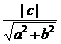 >1.∴c2>a2+b2. 答案:
C
>1.∴c2>a2+b2. 答案:
C
2.解析: 解法一:原等式化为2|z+ |=|z-i|,即动点到两定点的距离之比为不等于1的常数,所以动点轨迹是圆.
|=|z-i|,即动点到两定点的距离之比为不等于1的常数,所以动点轨迹是圆.
解法二:可设z=x+yi(x、y∈R),代入已知等式计算可得3x2+3y2+4x+2y=0,此方程为圆的方程. 答案: A
1.解析: 构造函数f(x)=logax-a-x,∵a>1,显然f(x)是(0,+∞)上的增函数,由a-x+logay<
a-y+logax logax-a-x>logay-a-y,∴x>y>0. 答案:
A
logax-a-x>logay-a-y,∴x>y>0. 答案:
A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com