
题目列表(包括答案和解析)
5.(理)直线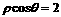 关于直线
关于直线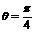 对称的直线的极坐标方程是 ( )
对称的直线的极坐标方程是 ( )
A.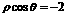 B.
B. C.
C.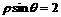 D.
D.
(文)把直线 沿y轴正方向平移1个单位,再关于原点对称后,所得直线
沿y轴正方向平移1个单位,再关于原点对称后,所得直线
的方程是 ( )
A.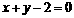 B.
B. C.
C.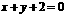 D.
D.
4.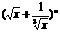 展开式的各项系数和大于8且小于32,则展开式中系数最大的项是( )
展开式的各项系数和大于8且小于32,则展开式中系数最大的项是( )
A.6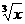 B.
B. C.
C.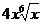 D.
D.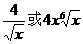
3.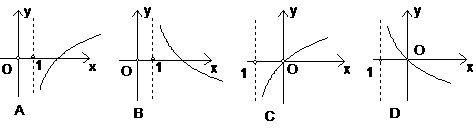 若函数
若函数 为增函数,那么
为增函数,那么 的图象是 ( )
的图象是 ( )
A. B. C. D.
2.如果复数z适合|z+2+2i|=|z|,那么|z-1+i|的最小值是 ( )
A.4 B. C.2 D.
C.2 D.
只有一项是符合要求的,请把正确答案的字母填在题后的括号内)
1.设集合A和集合B都是实数集R,映身f:A→B把集合A中的元素x映射到集合B中的
元素lg(x2+1),则在映射f下,象1的原象所成的集合是 ( )
A.{-1,1} B.{3,0} C.{3,-3} D.{3}
(17)(本小题满分12分)
(理)解关于x的不等式: ,(a>0且a≠1).
,(a>0且a≠1).
(文)解关于x的不等式: ,(a>0且a≠1).
,(a>0且a≠1).
(18)(本小题满分12分)
已知z1=3+4 ,z2=65
,z2=65
 且
且
(Ⅰ)求 ;
;
(Ⅱ)设z1、z2在复平面内所对应点分别为P、Q、O为坐标原点,以OP、OQ为边作
平行四边形OPRQ,求对角线OR的长及平行四边形OPRQ的面积.
(19)(本小题满分12分)
如图,已知四棱锥P-ABCD的侧面PAD与底面ABCD垂直,△PAD是边长为a的正三角形,ABCD为直角梯形, AB//CD,DC=2a,∠ADC=90°,∠DCB=45°,E为BP中
 点,F在PC上且PF=
点,F在PC上且PF=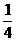 PC.
PC.
(Ⅰ)求证EF//平面PAD;
(Ⅱ)求三棱锥E-PCD的体积.
(20)(本小题满分12分,文科做(Ⅰ)、(Ⅱ),理科全做)
已知奇函数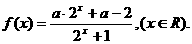
(Ⅰ)试确定实数a的值,并证明f(x)为R上的增函数;
(Ⅱ)记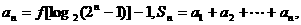 求
求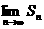 ;
;
(Ⅲ)若方程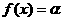 在(-∞,0)上有解,试证
在(-∞,0)上有解,试证 .
.
(21)(本小题满分12分)
某公司按现有能力,每月收入为70万元,公司分析部门测算,若不进行改革,入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元,以后逐月多减少2万元,如果进行改革,即投入技术改造300万元,且入世后每月再投入1万元进行员工培训,则测算得自入世后第一个月起累计收入Tn与时间n(以月为单位)的关系为Tn=an+b,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
(22)(本小题满分14分,文科只做(Ⅰ)、(Ⅱ),理科全做)
已知抛物线C: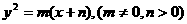 的焦点为原点,C的准线与直线
的焦点为原点,C的准线与直线
 的交点M在x轴上,
的交点M在x轴上, 与C交于不同的两点A、B,线段AB的垂直平分线交x轴于点N(p,0).
与C交于不同的两点A、B,线段AB的垂直平分线交x轴于点N(p,0).
(Ⅰ)求抛物线C的方程;
(Ⅱ)求实数p的取值范围;
(Ⅲ)若C的焦点和准线为椭圆Q的一个焦点和一条准线,试求Q的短轴的端点的轨迹方程.
22.(本题满分14分)
已知函数f(x)在(-1,1)上有定义, 且满足x、y∈(-1,1) 有
且满足x、y∈(-1,1) 有
 .
.
(Ⅰ)证明:f(x)在(-1,1)上为奇函数;
(Ⅱ)对数列 求
求 ;
;
(Ⅲ)(理)求证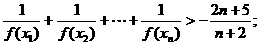
(文)求证
21.(本题满分12分)

A、B是两个定点,且|AB|=8,动点M到A点的距离
是10,线段MB的垂直平分线l交MA于点P,若以AB
所在直线为x轴,AB的中垂线为y轴建立直角坐标系.
(Ⅰ)试求P点的轨迹c的方程;
(Ⅱ)直线 与点P所在
与点P所在
曲线c交于弦EF,当m变化时,试求△AEF的面积的最大值.
20.(本题满分12分)
一家企业生产某种产品,为了使该产品占有更多的市场份额,拟在2001年度进行一系列的促销活动,经过市场调查和测算,该产品的年销量x万件与年促销费用t万元之间满足:
3-x与t+1(t≥0)成反比例,如果不搞促销活动,该产品的年销量只能是1万件,已知2001年生产该产品的固定投资为3万元,每生产1万件该产品需再投资32万元,当该产品的售价g(x)满足 时,则当年的产销量相等.
时,则当年的产销量相等.
(Ⅰ)将2001年的利润y表示为促销费t万元的函数;
(Ⅱ)该企业2001年的促销费投入多少万元时,企业的年利润最大?
(注:利润=收入-生产成本-促销费)
19.(文)(本题满分12分)
已知函数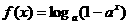 (其中a>0,且a≠1),解关于x的不等式
(其中a>0,且a≠1),解关于x的不等式
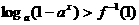
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com