
题目列表(包括答案和解析)
5.不等式 的解集是
( )
的解集是
( )
(A)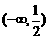 (B)
(B) (C)
(C) (D)
(D)
4.已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2等于 ( )
(A)-4 (B)-6 (C)-8 (D)-10
3.已知向量a=(3,4),b=(sinα,cosα),且a∥b,则tanα等于 ( )
(A) (B)
(B)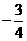 (C)
(C) (D)
(D)
2.由“p:8+7=16,q:π>3”构成的复合命题,下列判断正确的是 ( )
(A)p或q为真,p且q为假 ,非p为真 (B)p或q为假,p且q为假 ,非p为真
(C)p或q为真,p且q为假 ,非p为假 (D)p或q为假,p且q为真 ,非p为真
1.设全集U=R,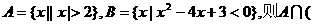
 B)是 ( )
B)是 ( )
(A) (B)
(B)
(C) (D)
(D)
22.(本小题满分14分)
已知圆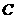 :
: 和圆
和圆 :
: ,现在构造一系列的圆
,现在构造一系列的圆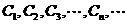 ,使圆
,使圆 同时与
同时与 和圆
和圆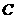 都相切,并都与OX轴相切.回答:
都相切,并都与OX轴相切.回答:
(1)求圆 的半径
的半径 ;
;
(2)证明:两个相邻圆 和
和 在切点间的公切线长为
在切点间的公切线长为 ;
;
(3)求和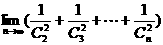 .
.
21. (本小题满分12分)
一列火车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),车上有一节邮政车厢,每停靠一站便要卸下前面各站发往该站的邮袋各一个,同时又要装上该站发往后面各站的邮袋各一个,试求:
(1)列车从第k站出发时,邮政车厢内共有邮袋数是多少个?
(2)第几站的邮袋数最多?最多是多少?
20.(本小题满分12分)
(理)设函数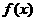 是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,
是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时, (a∈R).
(a∈R).
(1)当x∈(0,1]时,求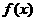 的解析式;
的解析式;
(2)若a>-1,试判断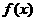 在(0,1]上的单调性,并证明你的结论;
在(0,1]上的单调性,并证明你的结论;
(3)是否存在a,使得当x∈(0,1]时,f(x)有最大值-6.
(文)已知 .
.
(1)求 之值;
之值;
(2)x为何值时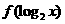 有最小值,并求其最小值.
有最小值,并求其最小值.
19.(本小题满分12分)
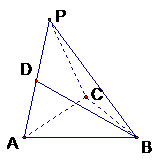
如图三棱锥P-ABC中,△ABC是正三角形,
∠PCA=90°,D为PA的中点,二面角P-AC
-B为120°,PC
= 2,AB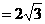 .
.
(Ⅰ)求证:AC⊥BD;
(Ⅱ)求BD与底面ABC所成角的正弦值.
18.(本小题满分12分)
(理)同时抛掷15枚均匀的硬币一次
(1) 试求至多有1枚正面向上的概率;
(2) 试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?请说明理由.
(文)已知: 、
、 、
、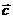 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 =(1,2)
=(1,2)
(Ⅰ)若|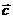 |
| ,且
,且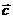 //
// ,求
,求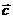 的坐标;
的坐标;
(Ⅱ)若| |=
|= 且
且 与
与 垂直,求
垂直,求 与
与 的夹角θ.
的夹角θ.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com