
题目列表(包括答案和解析)
(17)(本小题满分12分)
是否存在常数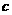 ,使得不等式
,使得不等式 对任意正数
对任意正数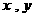 恒成立 , 试证明你的结论。
恒成立 , 试证明你的结论。
(18)(本小题满分12分)
在 中,A、B、C分别为三个内角,a、b、c分别为其对边,
中,A、B、C分别为三个内角,a、b、c分别为其对边, 外接圆半径为
外接圆半径为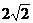 ,已知
,已知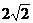
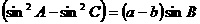 ;
;
(Ⅰ)求角C ;
(Ⅱ)求 面积S的最大值 .
面积S的最大值 .
(19)(本小题满分12分)
已知正项数列{an}和{bn}中,a1 = a ,(0<a<1=,b1=1-a,当n≥2且n∈ 时,an = an-1bn , bn =
时,an = an-1bn , bn = ,
,
(Ⅰ)证明:对任意n∈ ,都有an + bn =
1
,都有an + bn =
1
(Ⅱ)求数列 {an} 的通项公式
(Ⅲ)设Cn = a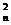 ·bn+1 , Sn为数列 {Cn}
的前n项和,求
·bn+1 , Sn为数列 {Cn}
的前n项和,求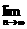 Sn 的值
Sn 的值
(20)(本小题满分12分)
如图,已知四棱锥P-ABCD中,面ABCD为正方形,PA⊥面ABCD,且PA = AB = a ,点M是PC的中点,
(Ⅰ)求异面直线BP与MD所成角的大小;
(Ⅱ)求二面角M-DA-C的大小.

(21)(本小题满分12分)
已知直线l: 与椭圆C:
与椭圆C: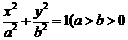 ,且b为整数)交于M、N两点,B为椭圆C短轴的上端点,若ΔMBN的重心恰为椭圆焦点F.
,且b为整数)交于M、N两点,B为椭圆C短轴的上端点,若ΔMBN的重心恰为椭圆焦点F.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C的左焦点为F’,问在椭圆C上是否存在一点P,使得∠F’PF = 60° ,证明你的结论.
(Ⅲ)是否存在斜率不为零的直线l,使椭圆C与直线l相交于不同的两点R、S,且 |BR| = |BS|,如果存在,求直线l在y轴上截距的取值范围;如果不存在,请说明理由.
(22)(本小题满分14分)
设x1、x2是函数f(x) =  x3+
x3+ x2-a2x
(a>0) 的两个极值点,且|x1|+|x2| = 2
x2-a2x
(a>0) 的两个极值点,且|x1|+|x2| = 2
(Ⅰ)证明:0<a≤1 ;
(Ⅱ)证明: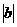 ≤
≤ ;
;
(Ⅲ)若函数h(x) = f′(x)-2a(x-x1),证明:当x1<x<2且x1<0时,|h(x)|≤4a .
(13)设集合A={5,log2(a+3)},集合B={a,b},若A∩B={2},则A∪B = ________________
(14)若不等式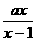 <1的解集为{x|x<1或x>2=,则实数a的值为________________
<1的解集为{x|x<1或x>2=,则实数a的值为________________
(15)曲线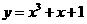 在点(1,3)处的切线方程是
在点(1,3)处的切线方程是
(16) 双曲线 的两个焦点为
的两个焦点为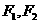 , P是此双曲线上一点,若PF1
, P是此双曲线上一点,若PF1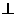 PF2 , 则点P到x轴的距离为_______________.
PF2 , 则点P到x轴的距离为_______________.
(1) 直线x + 3y-7= 0和kx-y-2 = 0与x轴、y轴的正半轴所围成的四边形有外接圆 , 则k为( )
(A) -3 ( B ) 6 ( C ) -6 ( D ) 3
(2)已知tan(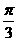 -α) =
-α) =  ,tan(
,tan(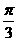 -β) =
-β) =  ,则tan(α-β)等于
( )
,则tan(α-β)等于
( )
(A) (B)-
(B)- (C)
(C)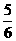 (D)-
(D)-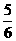
(3)设 、
、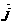 是不共线的单位向量,若
是不共线的单位向量,若 = 5
= 5 +3
+3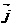 ,
, = 3
= 3 -5
-5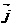 , 则
, 则 ⊥
⊥ 是
是 ⊥
⊥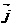 的 ( )
的 ( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既非充分又非必要条件
(4)已知平面α与平面β相交,直线m⊥α , 则 ( )
(A)β内必存在直线与m平行,且存在直线与m垂直
(B)β内不一定存在直线与m平行,也不一定存在直线与m垂直
(C)β内不一定存在直线与m平行,但必存在直线与m垂直
(D)β内必存在直线与m平行,但不一定存在直线与m垂直
(5)设函数f(x) = 3ax+1-2a ,在区间(-1,1)上存在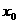 ,使f(x0) = 0 ,则实数a的取值范围是 ( )
,使f(x0) = 0 ,则实数a的取值范围是 ( )
(A)-1<a<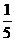 (B)a>
(B)a>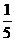 (C)a>
(C)a>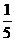 或a<-1 (D)a<-1
或a<-1 (D)a<-1
(6)复数Z满足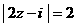 ,则
,则  的取值范围是
( )
的取值范围是
( )
(A) (B)
(B) (C)
(C) (D)
(D)
(7) 椭圆 (a> b >0) 有内接正n边形 ,则n的可能值是 ( )
(a> b >0) 有内接正n边形 ,则n的可能值是 ( )
(A) 4 (B) 3,4 (C) 3,4,5 (D) 3,4,6
(8)设一个正多面体的面数为F,顶点数为V,若F + V = 8,且它的各条棱长都等于4,则这一多面体的外接球的球面面积是 ( )
(A)12π (B)24π (C)16π (D)28π
(9)数列{an}中,a1 = 1 , 且an+1 = an +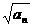 +
+ ,则a99等于
( )
,则a99等于
( )
(A)2004 (B)2005 (C)2400 (D)2500
(10)曲线C与函数 y = 2x-3 的图象关于直线 l : y = x 对称 ,则曲线 C 与 l 的一个交点的横坐标属于区间 ( )
(A)(-2,-1) (B)(2,3) (C)(1,2) (D)(-1,0)
(11)用四种不同颜色给一正方体的六个表面涂色,相邻两面涂不同颜色,则共有涂色方法有 ( )
(A)24种 (B)72种 (C)96种 (D)48种
(12)在曲线y = x3 + x – 2的切线中,与直线4x –y = 1平行的切线方程是 ( )
(A)4x –y = 0 (B)4x –y – 4 = 0
(C)2x –y – 2 = 0 (D)4x –y – 4 = 0 或 4x –y = 0
第Ⅱ卷(非选择题,共90分)
7. .8.
.8.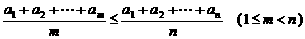 ,与
,与
 .
.
8.(2006年上海春季高考题)同学们都知道,在一次考试后,如果按顺序去掉一些高分,那么班级的平均分将降低;反之,如果按顺序去掉一些低分,那么班级的平均分将提高. 这两个事实可以用数学语言描述为:若有限数列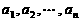 满足
满足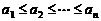 ,则
,则
(结论用数学式子表示).
答案 1. . 2.1. 3.16. 4.8. 5.1. 6.127.
. 2.1. 3.16. 4.8. 5.1. 6.127.
7. 在平面几何中:ΔABC的∠C内角平分线CE分AB所成线段的比为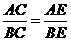 .把这个结论类比到空间:在三棱锥A-BCD中(如图)DEC平分二面角A-CD-B且与AB相交于E,则得到类比的结论是
.
.把这个结论类比到空间:在三棱锥A-BCD中(如图)DEC平分二面角A-CD-B且与AB相交于E,则得到类比的结论是
.

6.把一张长方形纸片按如图所示的方式连续对折,使每一次得到的折痕保持平行,这样对折7次后展开,问:长方形纸片中有_______条折痕.

第一次对折后 第二次对折后
5.对于函数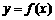 ,我们把使
,我们把使 的实数
的实数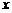 叫做函数
叫做函数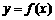 的零点.如果函数
的零点.如果函数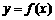 在区间
在区间 上的图象是连续不断的一条曲线,并且有
上的图象是连续不断的一条曲线,并且有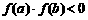 ,那么,我们就说函数
,那么,我们就说函数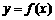 在区间
在区间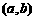 内有零点.则函数
内有零点.则函数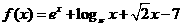 的零点有 个.
的零点有 个.
4.有两个同心圆,在外圆周上有不重合的4个点,在内圆周
上有不重合的2个点,由这6个点确定的直线的条数最少为_____.
3.如图,要用三根数据线将四台电脑A、B、C、D连接
起来以实现资源共享,则不同的连接方案共有 种(用数字作答).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com