18．(本小题满分12分)设数列{a_n}和{b_n}满足a₁=b₁=6, a₂=b₂=4, a₃=b₃=3, 且数列{a_n+1－a_n }(n∈N*)是等差数列，数列{b_n－2}(n∈N*)是等比数列.

　 (Ⅰ)求数列{a_n}和{b_n}的通项公式；

　 (Ⅱ)是否存在k∈N*，使a_k－b_k∈(0，)？若存在，求出k；若不存在，说明理由.

17．(本小题满分12分)某城市有甲、乙、丙3个旅游景点，一位客人游览这三个景点的概率分别是0.4，0.5，0.6，且客人是否游览哪个景点互不影响，设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.

(Ⅰ)求ξ的分布及数学期望；

(Ⅱ)记“函数f(x)＝x²－3ξx+1在区间[2，+∞上单调递增”为事件A，求事件A的概率.

16．已知n次式项式. 如果在一种算法中，计算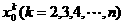的值需要k－1次乘法，计算P₃(x₀)的值共需要9次运算(6次乘法，3次加法)，那么计算P₁₀(x₀)的值共需要　　　　　　　 次运算.

下面给出一种减少运算次数的算法：P₀(x)=a₀，P_k+1(x)=xP_k(x)+a_k+1(k=0，1，2，…，n－1).利用该算法，计算P₃(x₀)的值共需要6次运算，计算P₁₀(x₀)的值共需要　　　　 次运算.

15．某公司有5万元资金用于投资开发项目，如果成功，一年后可获利12%，一旦失败，一年后将丧失全部资金的50%，下表是过去200例类似项目开发的实施结果：

则该公司一年后估计可获收益的期望

是__________(元)．

14．已知项数为8的等比数列的中间两项是方程的两根，则数列的各项积是　　　　　 ．

13．右图是某保险公司提供的资料，在1万元以上的保险单中，有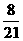少于2.5万元，那么不少于2.5万元的保险单有

　　　　　　　　 万元．

12．已知函数，下面四个图象中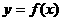的图象大致是　　　　　　　　　　　　　　　　 (　　 )

第Ⅱ卷(非选择题　 共90分)

11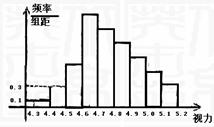．为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图，如右，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a, b的值分别为　 (　　 )

　　 A．0,27,78　　　　 B．0,27,83　　　　 C．2.7,78　　　　 D．2.7,83

10．将1，2，…，9这9个数平均分成三组，则每组的三个数都成等差数列的概率为(　　 )

　　　 A．　　　　　　　　　　 B．　　　　　　　　　　 C．　　　　　　　　　 D．

9．设函数满足，则方程根的个数可能是(　　 )

A．无穷个　　　　　 B．没有或者有限个　　 C．有限个　　　 D．没有或者无穷多