
题目列表(包括答案和解析)
15. (全国卷III)
在等差数列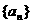 中,公差
中,公差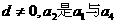 的等差中项.
的等差中项.
已知数列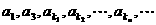 成等比数列,求数列
成等比数列,求数列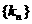 的通项
的通项
解:由题意得: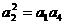 ……………1分
……………1分
即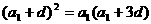 …………3分
…………3分
又
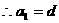 …………4分
…………4分
又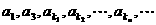 成等比数列,
成等比数列,
∴该数列的公比为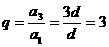 ,………6分
,………6分
所以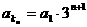 ………8分
………8分
又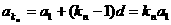 ……………………………………10分
……………………………………10分
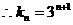 所以数列
所以数列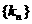 的通项为
的通项为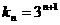 ……………………………12分
……………………………12分
14.(全国卷II)
已知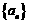 是各项为不同的正数的等差数列,
是各项为不同的正数的等差数列, 、
、 、
、 成等差数列.又
成等差数列.又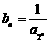 ,
,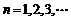 .
.
(Ⅰ) 证明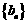 为等比数列;
为等比数列;
(Ⅱ) 如果无穷等比数列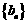 各项的和
各项的和 ,求数列
,求数列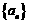 的首项
的首项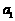 和公差
和公差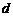 .
.
(注:无穷数列各项的和即当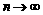 时数列前
时数列前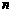 项和的极限)
项和的极限)
解:(Ⅰ)设数列{an}的公差为d,依题意,由
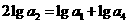 得
得
即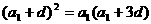 ,得
,得 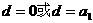 因
因
 当
当 =0时,{an}为正的常数列 就有
=0时,{an}为正的常数列 就有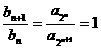
当 =
=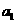 时,
时, ,就有
,就有

于是数列{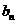 }是公比为1或
}是公比为1或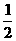 的等比数列
的等比数列
(Ⅱ)如果无穷等比数列 的公比
的公比 =1,则当
=1,则当 →∞时其前
→∞时其前 项和的极限不存在。
项和的极限不存在。
因而 =
=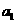 ≠0,这时公比
≠0,这时公比 =
=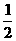 ,
,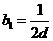
这样 的前
的前 项和为
项和为
则S=
由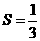 ,得公差
,得公差 =3,首项
=3,首项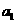 =
= =3
=3
13. (全国卷II) 已知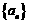 是各项为不同的正数的等差数列,
是各项为不同的正数的等差数列,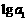 、
、 、
、 成等差数列.又
成等差数列.又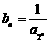 ,
,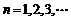 .
.
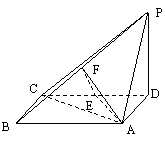 (Ⅰ) 证明
(Ⅰ) 证明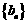 为等比数列;
为等比数列;
(Ⅱ) 如果数列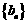 前3项的和等于
前3项的和等于 ,求数列
,求数列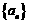 的首项
的首项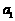 和公差
和公差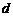 .
.
(I)证明:∵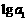 、
、 、
、 成等差数列
成等差数列
∴2 =
=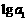 +
+ ,即
,即
又设等差数列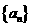 的公差为
的公差为 ,则(
,则(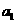 -
- )
)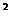 =
=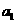 (
(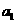 -3
-3 )
)
这样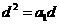 ,从而
,从而 (
( -
-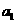 )=0
)=0
∵ ≠0
≠0
∴ =
=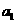 ≠0
≠0
∴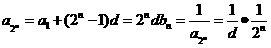
∴ 是首项为
是首项为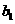 =
=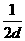 ,公比为
,公比为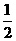 的等比数列。
的等比数列。
(II)解。∵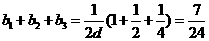
∴ =3
=3
∴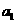 =
= =3
=3
12. (全国卷Ⅰ)
设等比数列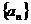 的公比为
的公比为 ,前n项和
,前n项和 。
。
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)设 ,记
,记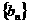 的前n项和为
的前n项和为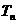 ,试比较
,试比较 与
与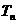 的大小。
的大小。
解:(Ⅰ)因为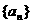 是等比数列,
是等比数列,
当
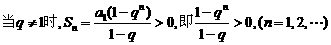
上式等价于不等式组: ①
①
或 ②
②
解①式得q>1;解②,由于n可为奇数、可为偶数,得-1<q<1.
综上,q的取值范围是
(Ⅱ)由 得
得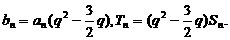
于是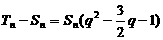
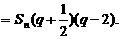
又∵ >0且-1<
>0且-1< <0或
<0或 >0
>0
当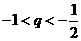 或
或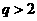 时
时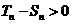 即
即
当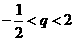 且
且 ≠0时,
≠0时, 即
即
当 或
或 =2时,
=2时, 即
即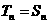
11. (全国卷Ⅰ) 设正项等比数列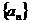 的首项
的首项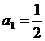 ,前n项和为
,前n项和为 ,且
,且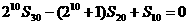 。
。
(Ⅰ)求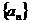 的通项;
的通项;
(Ⅱ)求 的前n项和
的前n项和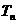 。
。
解:(Ⅰ)由  得
得 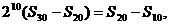
即
可得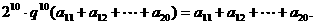
因为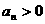 ,所以
,所以  解得
解得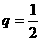 ,因而
,因而 
(Ⅱ)因为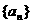 是首项
是首项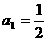 、公比
、公比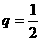 的等比数列,故
的等比数列,故

则数列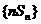 的前n项和
的前n项和 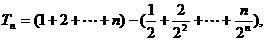
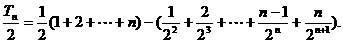
前两式相减,得 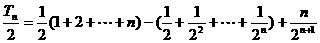
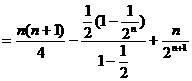 即
即 
10. (辽宁卷)已知函数 设数列
设数列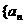 }满足
}满足 ,数列
,数列 }满足
}满足
(Ⅰ)用数学归纳法证明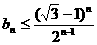 ;
;
(Ⅱ)证明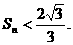
解:(Ⅰ)证明:当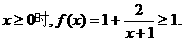 因为a1=1,
因为a1=1,
所以 ………………2分
………………2分
下面用数学归纳法证明不等式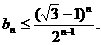
(1)当n=1时,b1= ,不等式成立,
,不等式成立,
(2)假设当n=k时,不等式成立,即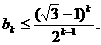
那么 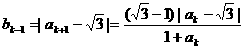 ………………6分
………………6分
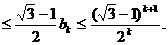
所以,当n=k+1时,不等也成立。
根据(1)和(2),可知不等式对任意n∈N*都成立。 …………8分
(Ⅱ)证明:由(Ⅰ)知,
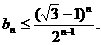
所以 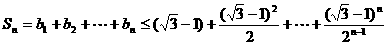
 …………10分
…………10分 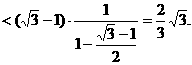
故对任意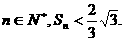 ………………(12分)
………………(12分)
9. (江苏卷)设数列{an}的前项和为 ,已知a1=1,
a2=6, a3=11,且
,已知a1=1,
a2=6, a3=11,且 ,
,  其中A,B为常数.
其中A,B为常数.
(Ⅰ)求A与B的值;
(Ⅱ)证明数列{an}为等差数列;
(Ⅲ)证明不等式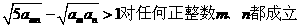 .
.
解:(Ⅰ)由 ,
,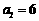 ,
,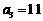 ,得
,得 ,
,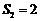 ,
, .
.
把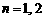 分别代入
分别代入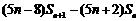
 ,得
,得
解得,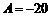 ,
,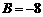 .
.
(Ⅱ)由(Ⅰ)知,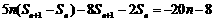 ,即
,即
 , ①
, ①
又 . ②
. ②
②-①得, ,
,
即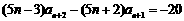 . ③
. ③
又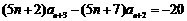 . ④
. ④
④-③得,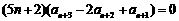 ,
,
∴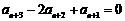 ,
,
∴ ,又
,又 ,
,
因此,数列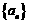 是首项为1,公差为5的等差数列.
是首项为1,公差为5的等差数列.
(Ⅲ)由(Ⅱ)知,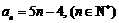 .考虑
.考虑
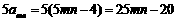 .
.
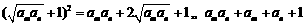
 .
.
∴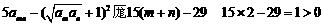 .
.
即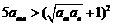 ,∴
,∴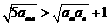 .
.
因此,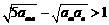 .
.
8. (湖南卷)自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量,n∈N*,且x1>0.不考虑其它因素,设在第n年内鱼群的繁殖量及捕捞量都与xn成正比,死亡量与xn2成正比,这些比例系数依次为正常数a,b,c.
(Ⅰ)求xn+1与xn的关系式;
(Ⅱ)猜测:当且仅当x1,a,b,c满足什么条件时,每年年初鱼群的总量保持不变?(不
要求证明)
(Ⅱ)设a=2,b=1,为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的
最大允许值是多少?证明你的结论.
解(I)从第n年初到第n+1年初,鱼群的繁殖量为axn,被捕捞量为bxn,死亡量为

(II)若每年年初鱼群总量保持不变,则xn恒等于x1, n∈N*,从而由(*)式得

因为x1>0,所以a>b.
猜测:当且仅当a>b,且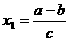 时,每年年初鱼群的总量保持不变.
时,每年年初鱼群的总量保持不变.
(Ⅲ)若b的值使得xn>0,n∈N*
由xn+1=xn(3-b-xn), n∈N*, 知
0<xn<3-b, n∈N*, 特别地,有0<x1<3-b. 即0<b<3-x1.
而x1∈(0, 2),所以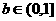
由此猜测b的最大允许值是1.
下证 当x1∈(0, 2) ,b=1时,都有xn∈(0, 2), n∈N*
①当n=1时,结论显然成立.
②假设当n=k时结论成立,即xk∈(0, 2),
则当n=k+1时,xk+1=xk(2-xk)>0.
又因为xk+1=xk(2-xk)=-(xk-1)2+1≤1<2,
所以xk+1∈(0, 2),故当n=k+1时结论也成立.
由①、②可知,对于任意的n∈N*,都有xn∈(0,2).
综上所述,为保证对任意x1∈(0, 2), 都有xn>0, n∈N*,则捕捞强度b的最大允许值是1.
7. (湖南卷)已知数列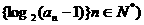 为等差数列,且
为等差数列,且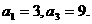
(Ⅰ)求数列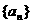 的通项公式;
的通项公式;
(Ⅱ)证明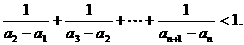
(I)解:设等差数列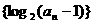 的公差为d.
的公差为d.
由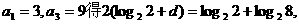 即d=1.
即d=1.
所以 即
即
(II)证明因为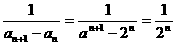 ,
,
所以
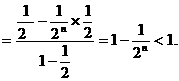
6. (湖北卷)已知不等式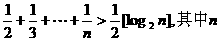 为大于2的整数,
为大于2的整数,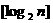 表示不超过
表示不超过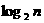 的最大整数. 设数列
的最大整数. 设数列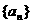 的各项为正,且满足
的各项为正,且满足
(Ⅰ)证明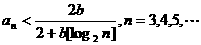
(Ⅱ)猜测数列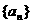 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)试确定一个正整数N,使得当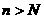 时,对任意b>0,都有
时,对任意b>0,都有
解:(Ⅰ)证法1:∵当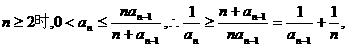
即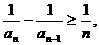
于是有 
所有不等式两边相加可得 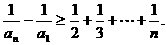
由已知不等式知,当n≥3时有,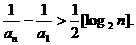
∵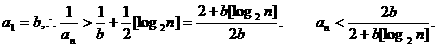
证法2:设 ,首先利用数学归纳法证不等式
,首先利用数学归纳法证不等式

(i)当n=3时, 由 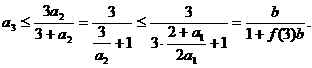
知不等式成立.
(ii)假设当n=k(k≥3)时,不等式成立,即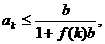
则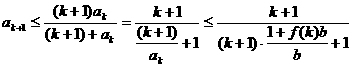

即当n=k+1时,不等式也成立.
由(i)、(ii)知,
又由已知不等式得 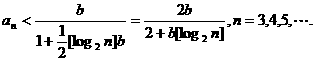
(Ⅱ)有极限,且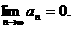
(Ⅲ)∵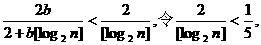
则有
故取N=1024,可使当n>N时,都有
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com