5.是的

　A．充分必要条件　　　　　　　　　　　　　　 B. 充分而不必要条件

　C．必要而不充分条件　　　　　　　　　　　　 D.既不充分也不必要条件

4．　 函数y=cosx，x∈[-的值域是

A．[0，1]　　　　　 B.[-1,1]　　　　　　 C.[0,　　　 D.[-

3．下列命题中，正确的是

A．　 如果一个平面内的两条直线与另一个平面平行，则这两个平面平行

B．　 如果一个平面内的无数条直线与另一个平面平行，则这两个平面平行

C．　 如果一个平面内的两条直线分别与另一个平面内的两条直线平行，则这两个平面平行

D．　 如果一个平面内的两条相交直线分别与另一个平面内的两条直线平行，则这两个平面平行

2.圆x²+y²=4与直线l:x=a相切，则a等于

A．2　　　　　　　　　　 B.2或-2　　　　　　 C.-2　　　　　　 D.4

1．　 设全集U=R,A={x|x＜2} ,B={x|x-1|≤3},则(C_UA)∩B=

A．[-2，4]　　　　　　 B.(-∞,-2]　　　　　 C.[2,4]　　　　 D.[2,+∞)

20．(本小题满分14分)

已知函数f (x) = x | x－a |(a∈R).

(I)判断f (x )的奇偶性；

(II)解关于x的不等式：f (x )≥2a²；

(III)写出f (x )的单调区间.

解：(I)函数f (x )的定义域是R，当a = 0时，f (－x ) =－x | －x| =－x | x | =－f (x )，

∴ f (x )是奇函数.

当a≠0时，∵ f (a ) = 0，f (－a ) = －2a | a |，

∴ f (－a )≠f (a )且f (－a )≠－f (a )，

∴ f (x )既不是奇函数，也不是偶函数.

(II)∵ x | x－a |≥2a²，

∴ 原不等式等价于　　 ①　 或　　 ②

由①得，无解；

由②得，即，

⑴ 当a = 0时，x≥0；

⑵ 当a＞0时，由，得x≥2a.

⑶当a＜0时，由，得x≥－a.

综上，当a≥0时，f (x )≥2a²的解集为{x| x≥2a}；当a＜0时，f (x )≥2a²的解集为{x| x≥－a}.

(III)f (x) = x | x－a | =.

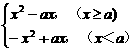⑴ a = 0时，如图1，函数f (x )在R上为单调递增函数，(－∞，+∞)为单调递增区间；

⑵ a＞0时，如图2，函数f (x )的单调递增区间为[a，+∞和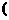－∞，]，单调递减区间为[，a]；

⑶ a＜0时，如图3，函数f (x )的单调递增区间为[，+∞和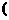－∞，a]，单调递减区间为[a，].

19．(本小题满分14分)

设数列{a_n}满足a₁ = 2，a_{n +1} = 3a_n－2，n = 1，2，3，….

(I)求证：数列{a_n－1}是等比数列；

(II)求{a_n}的通项公式；

(III)求{a_n}的前n项和S_n.

解：(I)证明：∵ a_{n +1} = 3a_n－2，且a₁ = 2，

∴ a_{n +1}－1 = 3 (a_n－1)，且a_n≠1，

∴ = 3，∴数列{a_n－1}是等比数列.

(II)∵数列{a_n－1}是等比数列，

∴ a_n－1 = (a₁－1)·q^n－1 = (2－1)·3^n－1 = 3^n－1，

∴ a_n = 3^n－1 + 1.

∴ {a_n}的通项公式a_n = 3^n－1 + 1.

(III)S_n = a₁ + a₂ + a₃ + … + a_n

　　　　　　　 = (3⁰ + 1) + (3 + 1) + (3² + 1) + … + (3^n－1 + 1)

　　　　　　　 = (3⁰ + 3 + 3² + … + 3^n－1 ) + n

　　　　　　　 =+ n =×3ⁿ + n－.

18．(本小题满分13分)

已知函数f (x ) = x² (ax + b )(a，b∈R)在x = 2时有极值，其图象在点 (1，f (1 ))处的切线与直线3x + y = 0平行.

(I)求a、b的值；

(II)求函数f (x )的单调区间.

解：(I)∵f (x ) = x² (ax + b ) = ax³ + bx²，

∴(x ) = 3ax² + 2bx，∵ 函数f (x )在x = 2时有极值，

∴ (2 ) = 0，即 12a + 4b = 0，　　　　　　　　　　　　　　　 ①

∵ 函数f (x )的图象在点(1，f (1 ))处的切线与直线3x + y = 0平行.

∴ (1 ) =－3，即3a + 2b =－3，　　　　　　　　　　　　　　 ②

由①②解得，a = 1，b =－3.

(II)(x ) = 3x²－6x = 3x (x－2)，令3x (x－2)＞0，

解得：x＜0或x＞2，

令3x (x－2)＜0，解得：0＜x＜2.

∴ 函数f (x )的单调递增区间为(－∞，0)和(2，+∞)，单调递减区间为(0，2).

17．(本小题满分13分)

在甲、乙两个队的乒乓球比赛中，乒乓球的规则是“五局三胜制”，现有甲、乙两队每局获胜的概率分别为和.

(I)前两局乙队以2：0领先，求最后甲、乙两队各自获胜的概率；

(II)乙队以3：2获胜的概率.

解：(I)在乙队以2：0领先的前提下，若甲队获胜则第三、四、五局均为甲队取胜，所以甲队获胜的概率为P₁ = ()³ =.

(方法1)在乙队以2：0领先的前提下，若乙队获胜则乙队可能以3：0；3：1；3：2的比分赢得比赛，所以乙队获胜的概率为：

　　　　　　　　 P₂ =+×+ ()²×=.

(方法2)“甲队获胜”与“乙队获胜”为对立事件，所以乙队获胜的概率为：

　　　　　　　　 P₂ = 1－=.

(II)若乙队以3：2获胜，则第五局为乙队取胜，前四局乙队输两局赢两局，所以乙队以3：2获胜的概率为：

　　　　　　　　 P₃ =·()²·()²·=.

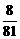16．(本小题满分14分)

已知四棱锥P－ABCD，底面是边长为1的正方形，侧棱PA⊥底面ABCD且PA = 1，M、N分别为AD、BC的中点，MQ⊥PD于Q.

(I)求证：AB∥平面MNQ；

(II)求证：平面PMN⊥平面PAD；

(III)求二面角P－MN－Q的余弦值.

解：(I)证明：∵ ABCD为正方形且M、N分别为AD、BC的中点，

∴ AB∥MN.

又∵ MN平面MNQ，AB平面MNQ，

∴ AB∥平面MNQ.

(II)证明：∵ ABCD为正方形且M、N分别为AD、BC的中点，

∴ MN⊥AD.

∵ PA⊥平面ABCD，MN平面ABCD，∴ MN⊥AP. 又∵ AD∩AP = A，

∴ MN⊥平面PAD，又∵ MN平面PMN，∴ 平面PMN⊥平面PAD.

(III)由(II)有MN⊥平面PAD，PM平面PAD，MQ平面PAD，

∴ MN⊥PM，MN⊥MQ，

∴ ∠PMQ为二面角P－MN－Q的平面角.

∵ PA = AD = 1，∴ ∠PDA =.

在Rt△MQD中，MQ =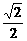MD =，在Rt△PAM中，PM ==.

在Rt△PMQ中，cos∠PMQ ===.

∴ 二面角P－MN－Q的余弦值为.