
题目列表(包括答案和解析)
9.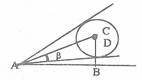 如图所示,有一广告气球,直径为6m,放在公司大楼上空,当行人仰望气球中心的仰角
如图所示,有一广告气球,直径为6m,放在公司大楼上空,当行人仰望气球中心的仰角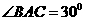 时,测得气球的视角
时,测得气球的视角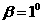 ,若
,若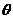 很小时可取
很小时可取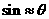 ,试估算该气球离地高度BC的值约为
( )
,试估算该气球离地高度BC的值约为
( )
A.72m B.86m C.102m D.118m
8.命题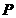 :函数
:函数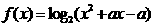 的值域为
的值域为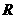 ,则
,则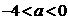 ;
;
命题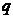 :函数
:函数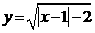 的定义域为
的定义域为 ,则 ( )
,则 ( )
A.“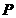 或
或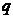 ”为假 B.“
”为假 B.“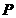 且
且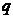 ”为真 C.
”为真 C.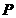 真
真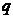 假 D.
假 D.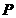 假
假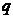 真
真
7.为了使函数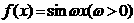 在区间
在区间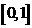 上至少出现50次最大值,则
上至少出现50次最大值,则 的最小值为
( )
的最小值为
( )
A.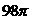 B.
B. 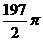 C.
C.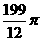 D.
D.
6.数列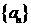 、
、 满足
满足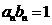 ,
,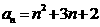 ,则数列
,则数列 的前10项和为( )
的前10项和为( )
A.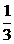 B.
B. 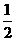 C.
C.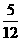 D.
D.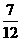
5.已知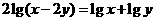 ,则
,则 的值为
( )
的值为
( )
A.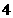 B.
B. 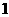 C.
C.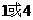 D.
D.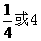
4.等比数列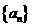 的各项均为正数,
的各项均为正数,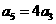 ,则
,则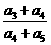 的值为
( )
的值为
( )
A.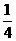 B.
B.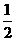 C.
C.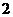 D.
D.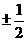
3.已知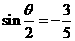 ,
,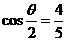 ,则
,则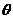 所在的象限为
( )
所在的象限为
( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2.“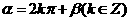 ”是“
”是“ ”的
( )
”的
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
1.已知集合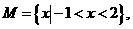
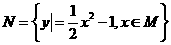 ,则
,则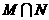 = ( )
= ( )
A.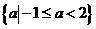 B.
B.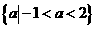 C.
C.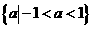 D.
D.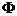
17 甲、乙两公司生产同一种产品,经测算,对于函数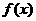 、
、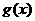 及任意的
及任意的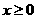 ,当甲公司投入
,当甲公司投入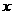 万元作宣传时,若乙公司投入的宣传费小于
万元作宣传时,若乙公司投入的宣传费小于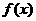 万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入
万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入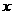 万元作宣传时,若甲公司投入的宣传费小于
万元作宣传时,若甲公司投入的宣传费小于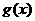 万元,则甲公司有失败的风险,否则无失败风险。
万元,则甲公司有失败的风险,否则无失败风险。
(Ⅰ)试解释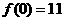 、
、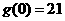 的实际意义;(Ⅱ)当
的实际意义;(Ⅱ)当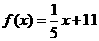 ,
,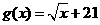 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用。问此时甲、乙两公司各应投入多少宣传费?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用。问此时甲、乙两公司各应投入多少宣传费?
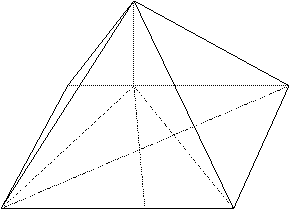 18 如图,四棱锥
18 如图,四棱锥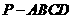 中,底面
中,底面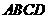 为平行四边形,
为平行四边形,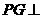 平面
平面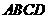 ,垂足为
,垂足为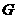 ,
,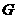 在边
在边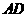 上,且
上,且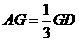 ,
,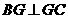 ,
, ,
,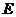 是边
是边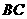 的中点,四面体
的中点,四面体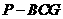 的体积是
的体积是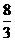 。
P
。
P
(Ⅰ)求异面直线 与
与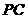 所成的角;
所成的角;
(Ⅱ)求点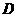 到平面
到平面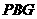 的距离;
A
G
D
的距离;
A
G
D
(Ⅲ)若点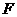 是棱
是棱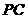 上一点且
上一点且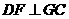 ,
,
求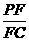 的值。
的值。
B E C
19已知数列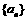 与
与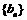 满足关系:
满足关系: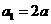 ,
,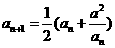 ,
,
(a>0)。
(Ⅰ)求数列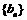 的通项公式并证明:
的通项公式并证明: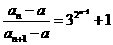 ;(Ⅱ)设
;(Ⅱ)设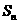 是数列
是数列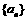 的前n项的和,当
的前n项的和,当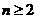 时
时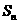 与
与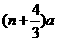 是否有确定的大小关系?若有则加以证明;若没有则说明理由。
是否有确定的大小关系?若有则加以证明;若没有则说明理由。
20从原点出发的某质点M,按照向量 移动的概率为
移动的概率为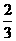 ,按照向量
,按照向量 移动的概率为
移动的概率为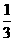 ,设M可到达点
,设M可到达点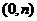 的概率为
的概率为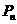 。
。
(Ⅰ)求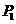 、
、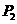 ; (Ⅱ)求证:
; (Ⅱ)求证: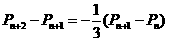 ;
(Ⅲ)求
;
(Ⅲ)求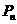 的表达式。
的表达式。
21已知点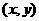 在椭圆
在椭圆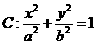 (a>b>0)的第一象限上运动。
(a>b>0)的第一象限上运动。
(Ⅰ)求点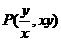 的轨迹
的轨迹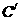 的方程;(Ⅱ)若把轨迹
的方程;(Ⅱ)若把轨迹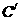 的方程表达式记为:
的方程表达式记为: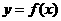 ,且在区间
,且在区间 内
内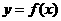 有最大值,试求椭圆
有最大值,试求椭圆 的离心率的取值范围。
的离心率的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com