
题目列表(包括答案和解析)
7、若把函数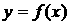 的图象按向量
的图象按向量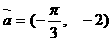 平移后,得到函数
平移后,得到函数 的图象,则原图象的函数解析式可以为 ( )
的图象,则原图象的函数解析式可以为 ( )
A. B.
B.
C. D.
D.
6. 若P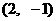 为圆
为圆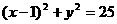 的弦AB的中点, 则直线AB的方程是 ( )
的弦AB的中点, 则直线AB的方程是 ( )
A. B.
B.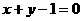
C. D.
D.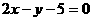
5、一所中学有高一、高二、高三学生共1600名,其中高三学生400名.如果通过分层抽样的方法从全体高中学生中抽取一个160人的样本,那么应当从高三年级的学生中抽取的人数是 ( )
A.20 B.40 C.60 D.80
4、一元二次方程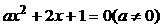 有一个正实数根和一个负实数根的充分不必要条件是
( )
有一个正实数根和一个负实数根的充分不必要条件是
( )
A. B.
B.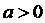 C.
C. D.
D.
2、已知函数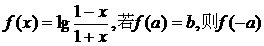 = ( )
= ( )
A.b B.-b C.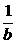 D.-
D.-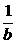
 3、函数
3、函数 的反函数的图象大致是
( )
的反函数的图象大致是
( )
1、cos600°= ( )
A.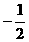 B.
B.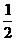 C.
C. D.
D.
(15)(本小题满分12分)
在⊿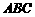 中,内角
中,内角 的对边分别是
的对边分别是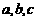 ,已知
,已知 .
.
(Ⅰ)试判断⊿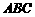 的形状;
的形状;
(Ⅱ)若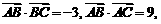 求角B的大小.
求角B的大小.
(16)(本小题满分14分)
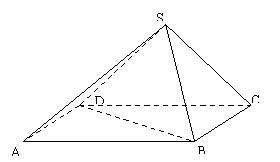
如图所示,在四棱锥 中,底面
中,底面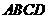 是矩形,侧面
是矩形,侧面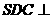 底面
底面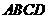 ,且
,且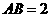 ,
,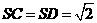 。
。
(Ⅰ)求证:平面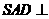 平面
平面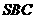 ;
;
(Ⅱ)设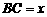 ,
,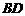 与平面
与平面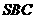 所成的角为
所成的角为 ,求
,求 的取值范围.
的取值范围.
(17)(本小题满分12分)
假设某批产品的正品率为 ,某检验员在检验这批产品时,把正品检验为正品的概率为
,某检验员在检验这批产品时,把正品检验为正品的概率为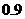 ,把次品检验为次品的概率为
,把次品检验为次品的概率为 .设“该检验员在检验这批产品时恰好将正品都检验为正品, 把次品都检验为次品”为事件A, 求事件A的概率
.设“该检验员在检验这批产品时恰好将正品都检验为正品, 把次品都检验为次品”为事件A, 求事件A的概率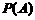 .
.
(18)(本小题满分14分)
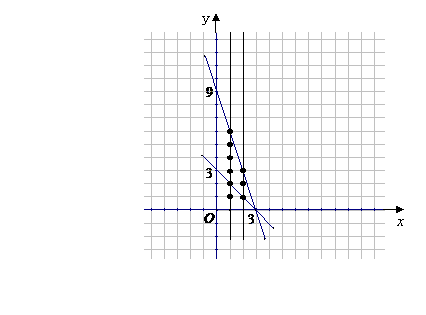
在平面直角坐标系上,设不等式组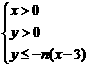 所表示的平面区域为
所表示的平面区域为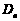 ,记
,记 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为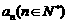 .
.
(Ⅰ)求
(Ⅱ)求数列 的通项公式
的通项公式 和前
和前 项和
项和 ;
;
 (Ⅲ)设数列
(Ⅲ)设数列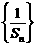 的前
的前 项和为
项和为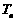 ,求
,求

(19)(本小题满分14分)
设抛物线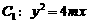
 的准线与
的准线与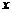 轴交于
轴交于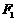 ,焦点为
,焦点为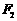 ;以
;以 为焦点,离心率
为焦点,离心率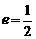 的椭圆
的椭圆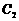 与抛物线
与抛物线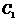 的一个交点为
的一个交点为 .
.
(Ⅰ)当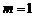 时,直线
时,直线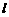 经过椭圆
经过椭圆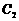 的右焦点
的右焦点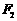 ,与抛物线
,与抛物线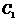 交于
交于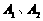 ,如果弦长
,如果弦长 等于三角形
等于三角形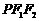 的周长,求直线
的周长,求直线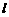 的斜率.
的斜率.
(Ⅱ)求最小实数 ,使得三角形
,使得三角形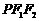 的边长是自然数.
的边长是自然数.

(20)(本小题满分14分)
(Ⅰ)已知函数: 求函数
求函数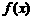 的最小值;
的最小值;
(Ⅱ)证明: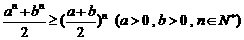 ;
;
(Ⅲ)定理:若 均为正数,则有
均为正数,则有 成立
成立
(其中 .请你构造一个函数
.请你构造一个函数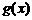 ,证明:
,证明:
当 均为正数时,
均为正数时,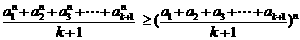 .
.
(11)在二项展开式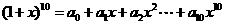 中,
中,
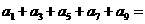 ______________.
______________.
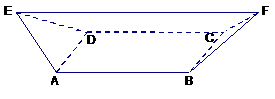 (12)如图,在多面体
(12)如图,在多面体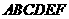 中,
中,
已知四边形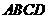 是边长为
是边长为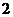 的正方
的正方
形,且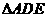 和
和 为正三角形,
为正三角形,
 ,
,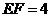 ,则
,则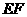 到平面
到平面
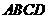 的距离为_______________.
的距离为_______________.
(13)已知数列 的前
的前 项和
项和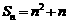 ,则
,则 ___________;
___________;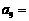 __________.
__________.
(14)若圆 :
:  与
与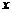 轴相切,则
轴相切,则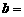 _______________;圆
_______________;圆 关于直线
关于直线 对称的圆
对称的圆 的方程是____________________.
的方程是____________________.
选择题答案
(1)复数 =
=
(A)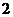 (B)
(B)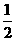 (C)
(C)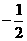 (D)
(D)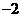
(2)设函数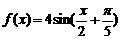 ,如果
,如果 ,则
,则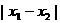 的最小值为
的最小值为
(A) (B)
(B) (C)
(C) (D)
(D)
(3)已知集合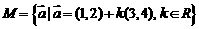 ,集合
,集合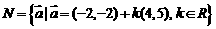
则
(A)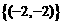 (B)
(B)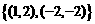 (C)
(C) (D)
(D)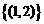
(4)方程 的根所在的区间是
的根所在的区间是
(A)(1,2) (B)(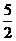 ,
,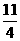 ) (C)(
) (C)(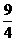 ,
,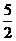 ) (D)(
) (D)( ,
, )
)
(5)下列图象中,有一个是函数 的导函数
的导函数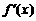 的图象,
的图象,
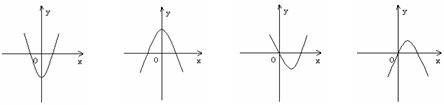
则
(A)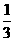 (B)
(B) (C)
(C) (D)
(D) 或
或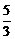
(6)设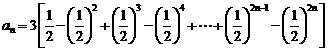 ,则数列
,则数列 是一个
是一个
(A) 无限接近1的递增数列 (B) 是一个各项为0的常数列
(C) 无限接近2的递增数列 (D) 是一个无限接近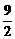 的递增数列
的递增数列
(7)已知定义在R上的偶函数f(x)的单调递减区间为[0,+∞ ,则不等式
,则不等式
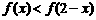 的解集是
的解集是
(A)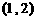 (B)
(B)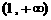 (C)
(C)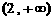 (D)
(D)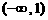
(8)已知双曲线 的右顶点为
的右顶点为 ,而
,而 是双曲线同一支上的两点,如果
是双曲线同一支上的两点,如果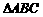 是正三角形,则
是正三角形,则
(A)  (B)
(B)  (C)
(C) 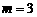 (D)
(D) 
(9)已知球面上有三点 ,
,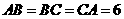 ,球心到平面
,球心到平面 的距离为
的距离为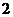 ,则球的半径为
,则球的半径为
(A)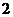 (B)
(B) (C)
(C) (D)
(D)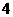
(10)椭圆 上有
上有 个不同的点
个不同的点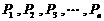 ,椭圆的右焦点为
,椭圆的右焦点为 ,数列
,数列 是公差大于
是公差大于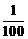 的等差数列,则n的最大值为
的等差数列,则n的最大值为
(A) 198 (B) 199 (C) 200 (D) 201
韶关市2006届高三第二次调研考试
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ部分1至2页,第Ⅱ部分3至8页。共150分。考试时间120分钟。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com