
题目列表(包括答案和解析)
1、设全集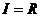 ,集合
,集合 ,
,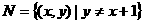 ,那么集合
,那么集合 等于( )
等于( )
(A)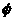 (B)
(B) (C)
(C) (D)
(D)
20、(本小题满分14分)
已知椭圆C的方程为: ,直线
,直线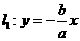 ,直线
,直线 ,过椭圆C的右焦点F作直线
,过椭圆C的右焦点F作直线 ,使
,使 ⊥
⊥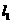 且
且 ∩
∩ =P.
=P.
(Ⅰ) 若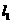 与
与 的夹角为60°,双曲线E以
的夹角为60°,双曲线E以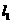 与
与 为渐近线,且双曲线E的焦距为4,求双曲线E的方程;
为渐近线,且双曲线E的焦距为4,求双曲线E的方程;
 (Ⅱ)若直线
(Ⅱ)若直线 与椭圆C的两个交点为A、B,且A在线段PF上,求
与椭圆C的两个交点为A、B,且A在线段PF上,求 的最大值.
的最大值.
2006高三3月份联考
19、(本小题满分14分)
已知函数 (a、b∈R)
(a、b∈R)
(Ⅰ)若x=2是方程 =0的一个根,
=0的一个根, 在[0,2]上是增函数,求证:
在[0,2]上是增函数,求证: ≤-2;
≤-2;
(Ⅱ) 设 图象上任意不同两点的连线的斜率为
图象上任意不同两点的连线的斜率为 ,若
,若 求
求 的取值范围.
的取值范围.
18、(本小题满分14分)
如图所示,  VAD是边长为2的等边三角形,ABCD是正方形, 平面VAD
VAD是边长为2的等边三角形,ABCD是正方形, 平面VAD 平面ABCD,E为VC中点.
平面ABCD,E为VC中点.
(Ⅰ)求VC与平面ABCD所成角的余弦值;
(Ⅱ)求D到平面VBC的距离;
 (Ⅲ)在边AB上是否存在一点F,使DE
(Ⅲ)在边AB上是否存在一点F,使DE 面VCF,若存在,求出点F的位置;若不存在,说明理由.
面VCF,若存在,求出点F的位置;若不存在,说明理由.
17、(本小题满分14分)
一台仪器每启动一次都随机地出现一个5位的二进制数 ,其中A的各位数字中,
,其中A的各位数字中, 出现
出现 的概率为
的概率为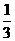 ,出现1的概率为
,出现1的概率为 .例如:A=10001,其中
.例如:A=10001,其中 .记
.记 ,当启动仪器一次时,
,当启动仪器一次时,
(Ⅰ)求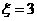 的概率;
的概率;
(Ⅱ)求 的概率分布列及
的概率分布列及 .
.
16、(本小题满分14分)
在数列{an}中,a1=tan ,
, .
.
(Ⅰ)写出a2,a3,a4;
(Ⅱ)猜想{an}的通项公式,并加以证明.
15、(本小题满分14分)
已知A、B、C的坐标分别为A(4,0)、B(0.4)、C(3cosα,3sinα)
(Ⅰ)若 ,且
,且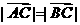 .求角α的值;
.求角α的值;
(Ⅱ)若 .求
.求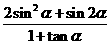 的值.
的值.
14.有女学生5名,男学生2名。现从中选4人到4个不同的社区服务,每个社区去1名学生,必须有男学生参加的安排方法种数是 ▲ (用数字作答).
13.在半径为6的球面上有A、B、C三点,若AB=2,∠ACB=30°,则球心O到平面ABC的距离为 ▲ .
12.设抛物线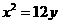 的焦点为F,经过点P(2,1)的直线
的焦点为F,经过点P(2,1)的直线 与抛物线相交于A、B两点且点P恰为AB的中点,则|AF|+|BF|= ▲ .
与抛物线相交于A、B两点且点P恰为AB的中点,则|AF|+|BF|= ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com