
题目列表(包括答案和解析)
5.如果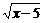 ≠kx对一切x≥15均成立,则有
≠kx对一切x≥15均成立,则有
A.k≤0 B.k≤0或k>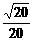 C.k≤0或k>
C.k≤0或k>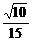 D.0≤k<
D.0≤k<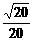
4.函数f(x)=b(1-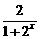 )+ a sinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在
)+ a sinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在
(-∞,0)上有
A.最大值10 B.最小值-5 C.最小值-4 D.最大值13
3. .已知|p|=2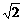 ,|q|=3,p、q的夹角为
,|q|=3,p、q的夹角为 ,如下图所示,若
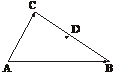
,如下图所示,若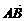 =5p+2q,
=5p+2q,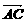 =p-3q,且D为BC的中点,则
=p-3q,且D为BC的中点,则 的长度为
的长度为
A.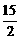 B.
B.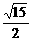 C.7 D.8
C.7 D.8
2. 下表是某市7个县级行政管理区人口数与土地面积:
|
行政区代号 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
人口(万) |
63.46 |
59.44 |
103.23 |
38.11 |
21.67 |
6.46 |
6.61 |
|
面积(万 km2) |
0.33 |
0.20 |
0.45 |
0.15 |
0.07 |
0.02 |
0.02 |
经统计比较可知,其中人口密度(人口/面积)最大的行政区是
A.x2 B.x3 C.x5 D.x7
1.一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是
A.81.2,4.4 B.78.8,4.4 C.81.2,84.4 D.78.8,75.6
21.解:由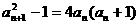 得,
得,

数列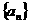 的各项为正值,
的各项为正值,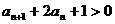
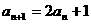
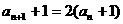
又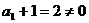
∴数列 为等比数列. ∴
为等比数列. ∴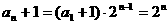 ,
, 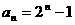 ,
,
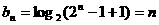
(2)设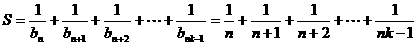
∴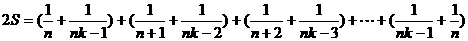 (1)
(1)
当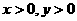 时,
时,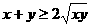 ,
,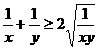
∴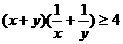 ,
,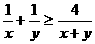 , 当且仅当
, 当且仅当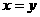 时等号成立.
时等号成立.
上述(1)式中, ,
,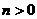 ,
,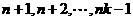 全为正,所以
全为正,所以
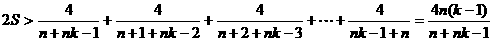
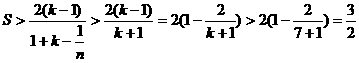
得证.
20.解:(1)双曲线的左准线为x=-1, 抛物线方程是
抛物线方程是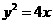 ;
;
(2)设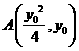 ,AP的直线方程为
,AP的直线方程为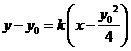 ,
,
将抛物线方程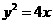 代入AP的直线方程,得
代入AP的直线方程,得 ,
,
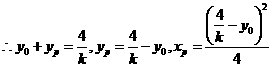 ,
,
同理: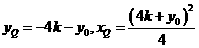 ,
,
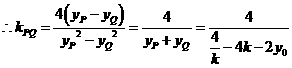 ,
,
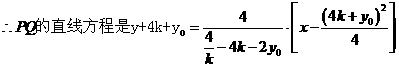 ,
,
令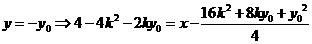 ,
,
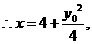
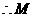 点的坐标是
点的坐标是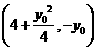 ,
,
∴存在h=4,使得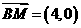 且
且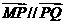
18.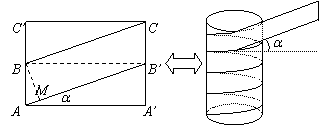 解 (1)缠绕角a显然与管子的直径、带子的宽度有关.
解 (1)缠绕角a显然与管子的直径、带子的宽度有关.
(2) 设管子的直径为D,带子的宽度为W.
把管子看作圆柱体,设想将侧面沿某一母线剪开后展开,其展开图如图所示.由题意,包扎时要使带子全部包住管道而且带子没有重叠的部分,这就意味着点B与B¢必在同一水平线上.
过点B作BM^AB¢,M为垂足,则BM=W;同时,AA¢=pD,∠A¢AB¢=a.
\在RtΔBMB¢中,sin a=BM:BB¢=W:pD
\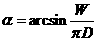
解: 19.(1)∵A1、A2重合于A
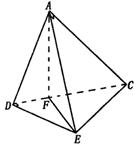 ∴AC⊥AD,AC⊥AE,故AC⊥面ADE ∴AC⊥DE
∴AC⊥AD,AC⊥AE,故AC⊥面ADE ∴AC⊥DE
∵A-DC-E为直二面角, ∴过A作AF⊥CD于F,则AF⊥面CDE,
故CD为AC在面CDE上的射影,由三垂线定理的逆定理有:CD⊥DE.
(2)∵AF⊥面CDE,∴∠AEF为AE与面DEC所成的角,
在Rt△CAD中,AD=2,AC=4,∴DC=2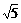 ,AF=
,AF=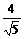 ,
,
又∵CD⊥DE,∴在正方形A1BA2C中,△DBE-△CA1D
故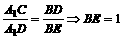 ,∴DE=
,∴DE=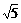 又∵DE⊥CD,DE⊥AC,∴DE⊥面ACD,则
又∵DE⊥CD,DE⊥AC,∴DE⊥面ACD,则
DE⊥AD,∴在Rt△ADE中,AE=3,故在Rt△AFE中,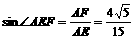 ∴AE与面DEC所成角的正弦值为
∴AE与面DEC所成角的正弦值为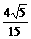 .
.
(3)设D到面AEC的距离为d,则由VD-AEC=VA-DEC有: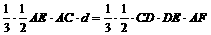
∴3×4d=2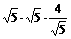 故
故 ,即点D到平面AEC的距离为
,即点D到平面AEC的距离为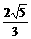 .
.
17.解:(1)由正弦定理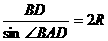 ,得
,得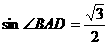 ,又由题意知
,又由题意知
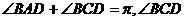 是锐角,∴
是锐角,∴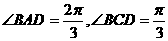
由余弦定理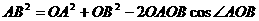 得
得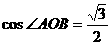
显然 是锐角,∴
是锐角,∴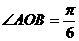 ,又圆心角
,又圆心角
∴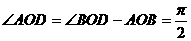
(2)易见三角形BCD是正三角形 ∴
∴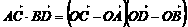
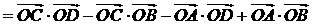
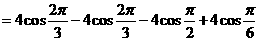

14.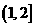 ;
;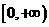 15.144 16.g(2),g(5),g(-2)
15.144 16.g(2),g(5),g(-2)
解析:由h(x)=f-1(x), h(x+1)=g-1(x), ∴g-1(x)=f-1(x+1)=y, 即x=g(y),x+1=f(y). ∴g(x)=f(x)-1.
∴g(2)=f(2)-1=4,g(5)=-3,g(-2)=7.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com