
题目列表(包括答案和解析)
4.对于函数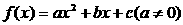 作
作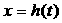 的代换,则总不改变函数
的代换,则总不改变函数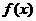 的值域的代换是 ( )
的值域的代换是 ( )
(A)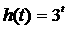 (B)
(B)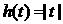 (C)
(C)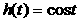 (D)
(D)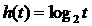
3.若存在实数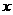 、
、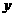 ,使得对于
,使得对于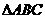 所在平面外一点
所在平面外一点 ,有
,有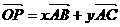 ,则有(
)
,则有(
)
(A)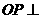 平面
平面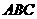 ;
(B)
;
(B)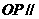 平面
平面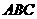 ;
;
(C)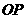 在平面
在平面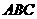 内; (D)点
内; (D)点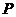 在直线
在直线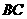 上.
上.
2.已知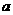 为正实数,奇函数
为正实数,奇函数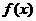 与直线
与直线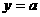 有两个交点,则方程
有两个交点,则方程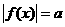 的实数根的个数是( )
的实数根的个数是( )
(A)1个 (B)2个 (C)3个 (D)4个
给出的四个选项中,只有一项是符合题目要求的.
1. 定义集合 A﹡B={x︱x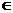 A且x
A且x B} 若A={1、2、3、4、5}
B} 若A={1、2、3、4、5}
B={2、4、5}则A﹡B的子集个数为( )
(A) 1 个 (B) 2个 (C) 3个 (D) 4个
21.(本小题满分16分)已知椭圆C1: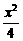 +y2=1的左、右顶点分别是A、B,点P是双曲线C2:
+y2=1的左、右顶点分别是A、B,点P是双曲线C2: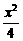 -y2=1在第一象限部分上的一点,连结AP交椭圆C1于点C,连结PB并延长交椭圆C1于点D.
-y2=1在第一象限部分上的一点,连结AP交椭圆C1于点C,连结PB并延长交椭圆C1于点D.
(1)若直线PA与PB的斜率分别为k1、k2,求证:k1·k2是定值;
(2)若△ACD与△PCD的面积相等,求直线CD的倾斜角;
(3)直线CD的倾斜角是否会随着点P的不同而改变?并说明理由.
20.(本小题满分16分)
已知集合A={(x,y)|y≥|x-a|},B={(x,y)|y≤-a|x|+2a}(a≥0).
(1)证明A∩B≠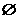 ;
;
(2)当0≤a≤4时,求由A∩B中点组成图形面积的最大值.
19.(本小题满分12分)
如图,给出了一个三角形数阵,已知每一列的数成等差数列,从第3行起,每一行的数成等比数列,每一行的公比都相等.记第i行第j列的数为aij(i≥j,i、j∈N*).
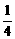
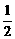 ,
,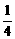
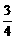 ,
,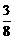 ,
,
……
(1)试写出aij关于i、j的表达式,并求a83;
(2)设这个数阵共有n行,求数阵表中的所有数之和.
18.(本小题满分14分)
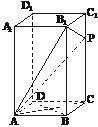
在正四棱柱ABCD-A1B1C1D1中,侧棱是底面边长的2倍,P是侧棱CC1上的一点.
(1)求证:不论P在侧棱CC1上何位置,总有BD⊥AP;
(2)若CC1=3C1P,求平面AB1P与平面ABCD所成的二面角的正切值;
(3)当P点在侧棱CC1上何处时,AP在平面B1AC上的射影是∠B1AC的平分线?
17.(本小题满分12分)
二人掷一颗骰子,两人各掷一次,点数大者为胜,但这个骰子可能不太规则,以致k点出现的概率是Pk(k=1,2,3,4,5,6).在这种情况下,
(1)求二人平局的概率P.
(2)证明P≥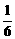 ;并证明如果P=
;并证明如果P=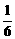 ,则Pk=
,则Pk=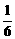 (k=1,2,3,4,5,6).
(k=1,2,3,4,5,6).
16.设x、y∈R,且满足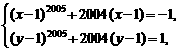 则x+y=___________.
则x+y=___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com