10.　 已知数列{bn}是等差数列,b1＝1,b1+b2+……+b10＝145. ①求数列{bn}的通项bn; ②设数列{an}的通项an＝loga(1+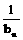)(其中a>0且a≠1),记Sn是数列{an}的前n项和.试比较Sn与的大小,并证明你的结论.(98年(25)12分)

9. 已知数列{a_n},{b_n}都是由正数组成的等比数列,公比分别为p,q,其中p＞q,且p≠1,q≠1.设c_n＝a_n+b_n,S_n为数列{c_n}的前项和,求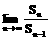.(97年(21)11分)

8. 设{a_n}是由正数组成的等比数列,S_n是其前n项和, Ⅰ.证明:(lgS_n+lgS_n+2)＜lgS_n+1; Ⅱ.是否存在常数c＞0,使得[lg(S_n－c)+lg(S_n+2－c)]＜lg(S_n+1－c)成立?并证明你的结论.(95年(25)12分)

7. 设{a_n}是正数组成的数列,其前n项的和为S_n,并且对所有的自然数n,a_n与2的等差中项等于S_n与2的等比中项, Ⅰ.写出数列{a_n}的前3项; Ⅱ.求数列{a_n}的通项公式(写出推导过程); Ⅲ.令b,(n∈N),求(b₁+b₂+……+b_n－n).(94年(25)14分)

6. 设等差数列{a_n}的前n项和为S_n,已知a₃＝12,S₁₂＞0,S₁₃＜0, Ⅰ.求公差d的取值范围; Ⅱ.指出S₁,S₂,……S₁₂中哪一个值最大,并说明理由.(92年(27)10分)

5. 有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数.(90年(21)10分)

4. 是否存在常数a,b,c,使得等式1·2²+2·3²+……+n(n+1)²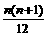＝(an²+bn+c)对一切自然数n成立？并证明你的结论.(89年(23)10分)

3. 设数列a₁,a₂,……a_n,……的前项和S_n与a_n的关系是S_n＝－ba_n+1－,其中b是与n无关的常数,且b≠－1, Ⅰ.求a_n和a_n+1的关系式; Ⅱ.写出用n和b表示a_n的表达式; Ⅲ.当0＜b＜1时,求极限S_n.(87年(20)12分)

2. 已知x₁＞0,x₁≠1,且x (n＝1,2,3……).试证:数列{x_n}或者对任意的自然数n都满足x_n＜x_n+1,或者对任意的自然数n都满足x_n+1＜x_n.(86年(22)12分)

1. 设a　 (n＝1,2,3……), Ⅰ.证明不等式对所有的正整数n都成立; Ⅱ.设b (n＝1,2,3……),用极限定义证明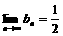.(85年(16)10分)