
题目列表(包括答案和解析)
8. 某班上午要排语文、数学、体育和英语四门功课,体育课不宜排在第一节或
第四节,且数学要排在语文的前边(不一定相邻),则不同的排课方案有( )
(A) 6种 (B) 12种 (C) 20种 (D) 24种
7. 若不等式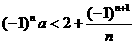 对
对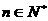 恒成立,则实数
恒成立,则实数 的取值范围是()
的取值范围是()
A. B.
B.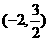 C.
C. D.
D.
6.求极限: = ( )
= ( )
(A)  (B) -
(B) -  (C)
(C)  (D)不存在
(D)不存在
5.正三棱锥 的侧棱长为1,底面边长为
的侧棱长为1,底面边长为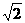 ,它的四个顶点在同一个球
,它的四个顶点在同一个球 的球面上,则球
的球面上,则球 的体积为
( )
的体积为
( )
A. B.
B. C.
C. D.
D.
4.下列命题中正确的是
(A) “直线a,b分别与直线c成等角”是“a // b”的充分条件;
(B) “平面α,β同垂直于平面γ”是“α//β”的充分条件 ;
(C) “直线a, b分别与平面α成等角”是“a // b”的必要条件;
(D) “直线a和平面α分别垂直于平面β”是“a //α”的充要条件;
3.一束光线经过点P(2,3)射到直线 x+y+1=0上,反射后穿过点Q(1,1),那么入射光线所在直线方程为( )
(A)5x+4y+2=0 (B)5x-4y+2=0 (C)5x-4y-2=0 (D)5x+4y-22=0
2.设 , 则此函数在区间
, 则此函数在区间  和
和 内分别为 ( )
内分别为 ( )
A.单调递增,单调递增 B.单调递增,单调递减
C.单调递减,单调递增 D.单调递减,单调递减
1.若  =
= ∈R,则
∈R,则 = ( )
= ( )
A. B.
B. C.
C.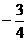 D.
D. .
.
21. 已知两圆A:
已知两圆A: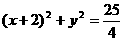 ,B:
,B: ,如图所示,动圆P与圆A和圆B都相外切,直线l的方程为x=a
(a
,如图所示,动圆P与圆A和圆B都相外切,直线l的方程为x=a
(a )
)
(1)求动圆P的圆心的轨迹方程,并证明:当a= 时,点P到点B的距离与到定直线l的距离之比为定值。
时,点P到点B的距离与到定直线l的距离之比为定值。
(2)延长PB与点P的轨迹交于另一点Q,求|PQ|的最值。
(3)延长PB与点P的轨迹交于另一点Q,如果存在某一位置,使得PQ的中点R在l上的射影C满足PC⊥QC,求a的取值范围。
.解:(1)设动圆P的半径为r,则|PA|=r+ ,|PB|=r+
,|PB|=r+ ,∴|PA|-|PB|=2,∴点P的轨迹是以A、B为焦点,焦距为4,实轴长为2的双曲线的右支,其方程为
,∴|PA|-|PB|=2,∴点P的轨迹是以A、B为焦点,焦距为4,实轴长为2的双曲线的右支,其方程为
若a= ,则l为双曲线的右准线,∴点P到点B的距离与到l的距离之比为双曲线的离心率e=2
,则l为双曲线的右准线,∴点P到点B的距离与到l的距离之比为双曲线的离心率e=2
(2)若PQ的斜率存在,设斜率为k,则直线PQ的方程为y=k(x-2),代入双曲线方程得(3-k2)x2+4k2x-4k2-3=0
由 ,解得k2>3
,解得k2>3
∴|PQ|=
当直线斜率不存在时,x1=x2=2得,y1=3,y2=-3,|PQ|=6
∴|PQ|的最小值为6
(3)当PC⊥QC时,P、C、Q构成直角三角形
∴R到直线l的距离|RC|= =xR-a
1
=xR-a
1
又点P、Q都在双曲线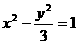 上
上
∴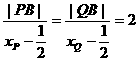 ,
,
即|PQ|=4xR-2,xR=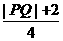 2
2
将②代入①得
|PQ|=2-4a≥6 ∴a≤-1
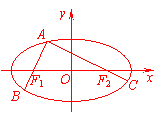
20.(本小题满分14分)设椭圆+=1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2.
(I)若∠AF1F2=α,∠AF2F1=β,试用α,β表示椭圆的离心率e;
(II)设→=λ1→,→=λ2→,当A在椭圆上运动时,求证:λ1+λ2为定值.
.解:(I)设F1(-c,0),F2(c,0).在△AF1F2中,由正弦定理得
==,
 即 |AF1|=,|AF2|=,
即 |AF1|=,|AF2|=,
所以 2a=|AF1|+|AF2|=+
=2c(+)=2c·,
得 e=.
(II)设A(x0,y0),B(x1,y1),C(x2,y2).
①当y0=0时,λ1+λ2=2=;当AB或AC与x轴垂直时,λ1+λ2=.
②当AB,AC都不与x轴垂直且y0≠0时,AC的方程为y=(x-c),
由消x得[b2(x0-c)2+a2y]y2+2b2y0(x0-c)y+c2b2y-a2b2y=0.
由韦达定理得 y2y0=,
所以 y2=,
所以 λ2==-=- ,
同理可得 λ1==-=-,
故 λ1+λ2=-[+]
=-===,
综上可知 λ1+λ2=.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com