
题目列表(包括答案和解析)
2.某校有40个班级,每班50人,每班选派3人参加“学代会”,在这个问题中样本容量是
A.40 B.50
C.120 D.150
解析:3×40=120.
答案:C
1.从50件产品中,采用逐一抽取的方法抽取5件产品,若其中只有一件次品,在送质检部门进行检验时次品被抽到的概率是
A.0.1 B.0.02
C.0或1 D.以上都不对
解析:次品被抽到的概率,即入样的概率p= =
= =0.1.
=0.1.
答案:A
22.有点难度哟!
(14分)(北京市东城区2004~2005学年第一学期期末教学目标检测)已知常数a>0,向量m=(0,a),n=(1,0),经过定点A(0,-a),以m+λn为方向向量的直线与经过定点B(0,a),以n+2λm为方向向量的直线相交于点P,其中λ∈R.
(1)求点P的轨迹C的方程;
(2)若a= ,过E(0,1)的直线l交曲线C于M、N两点,求
,过E(0,1)的直线l交曲线C于M、N两点,求 ·
·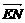 的取值范围.
的取值范围.
解:(1)设P点的坐标为(x,y),则 =(x,y+a),
=(x,y+a), =(x,y-a),
=(x,y-a),
又n=(1,0),m=(0,a),
故m+λn=(λ,a),n+2λm=(1,2λa).
由题知向量 与向量m+λn平行,故λ(y+a)=ax.
与向量m+λn平行,故λ(y+a)=ax.
又向量 与向量n+2λm平行,故y-a=2λax.
与向量n+2λm平行,故y-a=2λax.
两方程联立消去参数λ,得点P(x,y)的轨迹方程是(y+a)(y-a)=2a2x2, 即y2-a2=2a2x2.
(2)∵a= ,故点P的轨迹方程为2y2-2x2=1,
,故点P的轨迹方程为2y2-2x2=1,
此时点E(0,1)为双曲线的焦点.
①若直线l的斜率不存在,其方程为x=0,l与双曲线交于M(0, )、N(0,-
)、N(0,- ),
),
此时 ·
·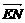 =(
=( -1)(-
-1)(- -1)=1-
-1)=1- =
= .
.
②若直线l的斜率存在,设其方程为y=kx+1,代入2y2-2x2=1化简得2(k2-1)x2+4kx+1=0.
∵直线l与双曲线交于两点,
∴Δ=(4k)2-8(k2-1)>0且k2-1≠0.
解得k≠±1.
设两交点为M(x1,y1)、N(x2,y2),
则x1+x2=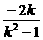 ,x1x2=
,x1x2= .
.
此时 ·
·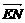 =(x1,y1-1)·(x2,y2-1)=(x1,kx1)·(x2,kx2)
=(x1,y1-1)·(x2,y2-1)=(x1,kx1)·(x2,kx2)
=x1x2+k2x1x2=(k2+1)x1x2
=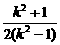 =
= (1+
(1+ ).
).
当-1<k<1时,k2-1<0,故 ·
·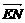 =
= (1+
(1+ )≤-
)≤- ;
;
当k>1或k<-1时,k2-1>0,
故 ·
·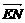 =
= (1+
(1+ )>
)> .
.
综上所述, ·
·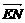 的取值范围是(-∞,-
的取值范围是(-∞,- )∪[
)∪[ ,+∞).
,+∞).
21.有点难度哟!
(12分)(2004年全国Ⅱ,21)给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点.
(1)设l的斜率为1,求 与
与 夹角的大小;
夹角的大小;
(2)设 =λ
=λ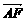 ,若λ∈[4,9],求l在y轴上截距的变化范围.
,若λ∈[4,9],求l在y轴上截距的变化范围.
分析:本题主要考查抛物线的性质、直线与抛物线的关系以及解析几何的基本方法、思想和综合解题能力.
解:(1)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为y=x-1.
将y=x-1代入方程y2=4x,并整理得
x2-6x+1=0.设A(x1,y1),B(x2,y2),则有x1+x2=6,x1x2=1.
 ·
· =(x1,y1)·(x2,y2)
=(x1,y1)·(x2,y2)
=x1x2+y1y2=2x1x2-(x1+x2)+1
=-3.
| ||
|| |=
|= ·
·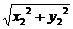
= =
=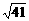 .
.
cos〈 ,
, 〉=
〉=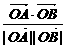 =-
=- .
.
所以 与
与 夹角的大小为
夹角的大小为
π-arccos .
.
(2)由题设 =λ
=λ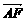 ,得
,得
(x2-1,y2)=λ(1-x1,-y1),
|
 x2-1=λ(1-x1),
①
x2-1=λ(1-x1),
①
y2=-λy1. ②
由②得y22=λ2y12.
∵y12=4x1,y22=4x2,∴x2=λ2x1. ③
联立①③解得x2=λ.依题意有λ>0,
∴B(λ,2 )或B(λ,-2
)或B(λ,-2 ).又F(1,0),得直线l方程为(λ-1)y=2
).又F(1,0),得直线l方程为(λ-1)y=2 (x-1)或(λ-1)y=-2
(x-1)或(λ-1)y=-2 (x-1).
(x-1).
当λ∈[4,9]时,l在y轴上的截距为 或-
或- .由
.由 =
= +
+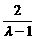 ,
,
可知 在[4,9]上是递减的,
在[4,9]上是递减的,
∴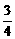 ≤
≤ ≤
≤ ,-
,- ≤-
≤- ≤-
≤-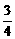 .
.
直线l在y轴上截距的变化范围为[- ,-
,-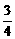 ]∪[
]∪[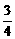 ,
, ].
].
20.(12分)(2003年北京朝阳区模拟题)已知椭圆C: +
+ =1(a>b>0).
=1(a>b>0).
(1)若点P(x0,y0)是椭圆C内部的一点,求证: +
+ <1;
<1;
(2)若椭圆C: +
+ =1(a>b>0)上存在不同的两点关于直线l:y=x+1对称,试求a、b满足的关系式.
=1(a>b>0)上存在不同的两点关于直线l:y=x+1对称,试求a、b满足的关系式.
(1)证明:设F1、F2为椭圆C的左、右两个焦点.∵P是椭圆C内部的一点,
∴|F1P|+|F2P|<2a.
∴ +
+ <2a.
<2a.
∴(a2-c2)x02+a2y02<a2(a2-c2).
∴ +
+ <1(b2=a2-c2).
<1(b2=a2-c2).
(2)解:设椭圆C上关于直线l对称的点A、B的坐标为A(x1,y1)、B(x2,y2),线段AB的中点坐标为M(xM,yM),则有
 b2x12+a2y12=a2b2,
①
b2x12+a2y12=a2b2,
①
b2x22+a2y22=a2b2, ②
 =-1, ③
=-1, ③
yM=xM+1. ④
②-①得b2(x22-x12)+a2(y22-y12)=0,
b2(x2-x1)(x2+x1)+a2(y2-y1)(y2+y1)=0,
b2xM+a2yM =0,
=0,
把③代入上式得b2xM-a2yM=0, ⑤
由④和⑤得xM= ,yM=
,yM= ,
,
即M( ,
, ).
).
∵点M在椭圆C的内部,
∴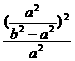 +
+ <1.
<1.
∴a2+b2<(b2-a2)2=(a+b)2(a-b)2.
a、b应满足的不等式为a2+b2<(a+b)2(a-b)2.
19.(12分)(2004年春季上海)设点P(x,y)(x≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点),点P到定点M( ,0)的距离比点P到y轴的距离大
,0)的距离比点P到y轴的距离大 .
.
(1)求点P的轨迹方程,并说明它表示什么曲线;
(2)若直线l与点P的轨迹相交于A、B两点,且OA⊥OB,点O到直线l的距离为 ,求直线l的方程.
,求直线l的方程.
解:(1)∵x≥0,∴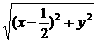 =x+
=x+ .
.
整理得y2=2x.
这就是动点P的轨迹方程,它表示顶点在原点,对称轴为x轴,开口向右的一条抛物线.
(2)①当直线l的斜率不存在时,由题设可知,直线l的方程是x= .
.
联立x= 与y2=2x,可求得点A、B的坐标分别为(
与y2=2x,可求得点A、B的坐标分别为( ,
, )与(
)与( ,-
,- ),此时不满足OA⊥OB,故不合题意.
),此时不满足OA⊥OB,故不合题意.
②当直线l的斜率存在时,可设直线l的方程为y=kx+b(其中k≠0,b≠0).
将x= 代入y2=2x中,
代入y2=2x中,
并整理得ky2-2y+2b=0. ①
设直线l与抛物线的交点坐标为A(x1,y1)、B(x2,y2),则y1、y2为方程①的两个根,于是y1y2= .
.
又由OA⊥OB可得x1x2+y1y2=0. ②
将x1= ,x2=
,x2=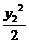 代入②并整理得y1y2+4=0,∴b+2k=0. ③
代入②并整理得y1y2+4=0,∴b+2k=0. ③
又由点O到直线l的距离为 ,得
,得 =
= . ④
. ④
联立③④得k=1,b=-2或k=-1,b=2.
故直线l的方程为y=x-2或y=-x+2.
18.(12分)已知椭圆的焦点是F1(-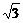 ,0)和F2(
,0)和F2(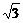 ,0),离心率为e=
,0),离心率为e= .
.
(1)求椭圆上的点到直线2x+3y+8=0距离的最大值;
(2)若P在椭圆上, ·
· =
=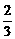 ,求△PF1F2的面积.
,求△PF1F2的面积.
解:(1)设椭圆 +
+ =1,半焦距为c,则
=1,半焦距为c,则
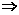
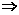


 c=
c=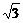 a=2
a2=4,
a=2
a2=4,
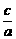 =
= a2-b2=3 b2=1.
a2-b2=3 b2=1.
∴椭圆方程为 +y2=1.
+y2=1.
设椭圆上的点为P(2cosθ,sinθ),
P到直线2x+3y+8=0的距离d=|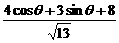 |=|
|=| |≤|
|≤| |=
|= .
.
当且仅当sin(θ+ )=1时取“=”(其中tan
)=1时取“=”(其中tan =
= ).
).
椭圆上的点到直线2x+3y+8=0的最大值为 .
.
(2)∵ ·
· =|
=| ||
|| |cos〈
|cos〈 ,
, 〉=
〉=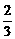 ,
,
又∵| |2=|
|2=| |2+|
|2+| |2-2|
|2-2| |·|
|·| |cos〈
|cos〈 ,
, 〉,
〉,
∴|PF1|+|PF2|=4,
即12=(| |+|
|+| |)2-2|
|)2-2| |·|
|·| |-
|-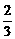 ·2=16-2|
·2=16-2| |·|
|·| |-
|-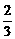 ·2
·2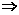 ?|
?| |·|
|·| |=
|=
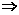 cos〈
cos〈 ,
, 〉=
〉=
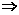 sin〈
sin〈 ,
, 〉=
〉= .
.
∴S△PF F
F =
= |
| ||
|| |sin〈
|sin〈 ,
, 〉=
〉= ·
· ·
· =
=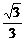 .
.
17.(12分)(2005年北京海淀区第一学期期末练习)设椭圆 +
+ =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
(1)求直线l和椭圆的方程;
(2)求证:点F1(-2,0)在以线段AB为直径的圆上;
(3)在直线l上有两个不重合的动点C、D,以CD为直径且过点F1的所有圆中,求面积最小的圆的半径长.
(1)解:直线l:y=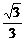 (x+3),
(x+3),
由已知c=2及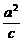 =3,
=3,
解得a2=6,∴b2=6-22=2.
∴椭圆方程为 +
+ =1.
=1.
|
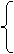 x2+3y2-6=0, ①
x2+3y2-6=0, ①
y=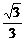 (x+3),
②
(x+3),
②
将②代入①,整理得2x2+6x+3=0. ③
设A(x1,y1)、B(x2,y2),则x1+x2=-3,x1x2= .
.
方法一:k ·k
·k =
= ·
·
=
=
=-1,
∴F1A⊥F1B,即∠AF1B=90°.
∴点F1(-2,0)在以线段AB为直径的圆上.
方法二: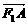 ·
· =(x1+2,y1)·(x2+2,y2)
=(x1+2,y1)·(x2+2,y2)
=(x1+2)(x2+2)+y1y2
=x1x2+2(x1+x2)+4+ [x1x2+3(x1+x2)+9]
[x1x2+3(x1+x2)+9]
= x1x2+3(x1+x2)+7=0,
x1x2+3(x1+x2)+7=0,
∴F1A⊥F1B.则∠AF1B=90°.
∴点F1(-2,0)在以线段AB为直径的圆上.
(3)解:面积最小的圆的半径长应是点F1到直线l的距离,设为r.
∴r= =
= 为所求.
为所求.
16.(2004年春季上海)若平移椭圆4(x+3)2+9y2=36,使平移后的椭圆中心在第一象限,且它与x轴、y轴分别只有一个交点,则平移后的椭圆方程是_____________.
解析:由题意知椭圆的长半轴长a=3,短半轴长b=2,因椭圆与x轴、y轴只有一个交点,故椭圆与x轴、y轴相切,椭圆的中心为(3,2),所以椭圆方程为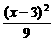 +
+ =1.
=1.
答案: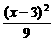 +
+ =1
=1
15.(2005年黄冈市调研,15)在△ABC中,B(-2,0)、C(2,0)、A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下面给出了一些条件及方程,请你用线把左边△ABC满足的条件及相应的右边A点的轨迹方程连起来.(错一条连线得0分)
①△ABC周长为10 a y2=25
②△ABC面积为10 b x2+y2=4(y≠0)
③△ABC中,∠A=90°
c  +
+ =1(y≠0)
=1(y≠0)
解析:①由|AB|+|AC|=6,得 +
+ =1(y≠0).
=1(y≠0).
②由 |BC||y|=10,得y2=25.
|BC||y|=10,得y2=25.
③由|AB|2+|AC|2=|BC|2,得x2+y2=4(y≠0).
答案:①→c ②→a ③→b
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com