
题目列表(包括答案和解析)
6.已知复数(x-2)+yi(x、y∈R)的模为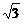 ,则
,则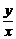 的最大值是
的最大值是
A.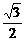 B.
B.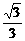 C.
C.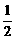 D.
D.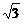
解析:∵|x-2+yi|=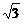 ,
,
∴(x-2)2+y2=3.
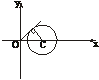
∴(x,y)在以C(2,0)为圆心、以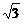 为半径的圆上,如右图,由平面几何知识知
为半径的圆上,如右图,由平面几何知识知 .
.
答案:D
5.已知复平面内的圆M:|z-2|=1,若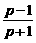 为纯虚数,则与复数p对应的点P
为纯虚数,则与复数p对应的点P
A.必在圆M上 B.必在圆M内
C.必在圆M外 D.不能确定
解析:∵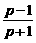 为纯虚数,设为ki(k∈R,k≠0),
为纯虚数,设为ki(k∈R,k≠0),
∴(1-ki)p=1+ki,取模得|p|=1且p≠1.
∴选C.
答案:C
4.设f(n)=(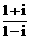 )n+(
)n+(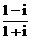 )n(n∈Z),则集合{x|x=f(n)}中元素的个数是
)n(n∈Z),则集合{x|x=f(n)}中元素的个数是
A.1 B.2 C.3 D.无穷多个
解析:∵f(n)=in+(-i)n,
∴f(0)=2,f(1)=i-i=0,f(2)=-1-1=-2,f(3)=-i+i=0.
∴{x|x=f(n)}={-2,0,2}.
答案:C
3.在下列命题中,正确命题的个数为
①两个复数不能比较大小;
②z1、z2、z3∈C,若(z1-z2)2+(z2-z3)2=0,则z1=z3;
③若(x2-1)+(x2+3x+2)i是纯虚数,则实数x=±1;
④z为虚数的一个充要条件是z+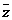 ∈R;
∈R;
⑤若a、b是两个相等的实数,则(a-b)+(a+b)i是纯虚数;
⑥复数z∈R的一个充要条件是z=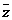 .
.
A.0 B.1 C.2 D.3
解析:①错,两个复数如果都是实数则可比较大小;②错,当z1、z2、z3不全是实数时不成立,如z1=i,z2=1+i,z3=1时满足条件,但z1≠z3;③错,当x=-1时,虚部也为零,原数是实数;④错,此条件是必要非充分条件;⑤错,当a=b=0时,原数是实数;⑥对.
答案:B
2.当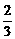 <m<1时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于
<m<1时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:z对应的点为(3m-2,m-1),
∵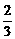 <m<1,
<m<1,
∴0<3m-2<1,-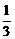 <m-1<0.
<m-1<0.
答案:D
1.如果复数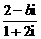 (其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
(其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
A.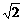 B.
B.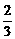 C.-
C.-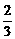 D.2
D.2
解析: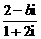 =
=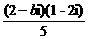 =
=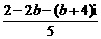
∴2-2b=b+4,b=-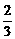 .
.
答案:C
22.(14分)设函数y=f(x)定义在R上,对任意实数m、n,恒有f(m+n)=f(m)·
f(n)且当x>0时,0<f(x)<1.
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减;
(3)设集合A={(x,y)|f(x2)·f(y2)>f(1)},B={(x,y)|f(ax-y+2)=1,
a∈R},若A∩B=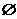 ,求a的取值范围.
,求a的取值范围.
(1)证明:在f(m+n)=f(m)f(n)中,
令m=1,n=0,得f(1)=f(1)f(0).
∵0<f(1)<1,∴f(0)=1.
设x<0,则-x>0.令m=x,n=-x,代入条件式有f(0)=f(x)·f(-x),而f(0)=1,
∴f(x)=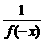 >1.
>1.
(2)证明:设x1<x2,则x2-x1>0,
∴0<f(x2-x1)<1.
令m=x1,m+n=x2,
则n=x2-x1,代入条件式,得
f(x2)=f(x1)·f(x2-x1),
即0<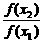 <1.∴f(x2)<f(x1).
<1.∴f(x2)<f(x1).
∴f(x)在R上单调递减.
(3)解:由f(x2)·f(y2)>f(1)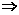 f(x2+y2)>f(1).
f(x2+y2)>f(1).
又由(2)知f(x)为R上的减函数,
∴x2+y2<1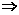 点集A表示圆x2+y2=1的内部.
点集A表示圆x2+y2=1的内部.
由f(ax-y+2)=1得ax-y+2=0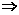 点集B表示直线ax-y+2=0.
点集B表示直线ax-y+2=0.
∵A∩B=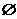 ,∴直线ax-y+2=0与圆x2+y2=1相离或相切.
,∴直线ax-y+2=0与圆x2+y2=1相离或相切.
于是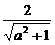 ≥1
≥1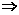 -
-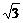 ≤a≤
≤a≤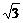 .
.
21.(12分)设f(x)是定义在R上的偶函数,其图象关于直线x=1对称,对任意x1、x2∈[0,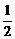 ],都有f(x1+x2)=f(x1)·f(x2).
],都有f(x1+x2)=f(x1)·f(x2).
(1)设f(1)=2,求f(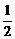 ),f(
),f(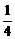 );
);
(2)证明f(x)是周期函数.
(1)解:由f(x1+x2)=f(x1)·f(x2),x1、x2∈[0,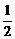 ]知f(x)=f(
]知f(x)=f(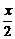 )·f(
)·f(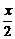 )=[f(
)=[f(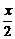 )]2≥0,x∈[0,1].
)]2≥0,x∈[0,1].
因为f(1)=f(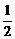 )·f(
)·f(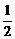 )=[f(
)=[f(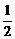 )]2,及f(1)=2,所以f(
)]2,及f(1)=2,所以f(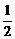 )=2
)=2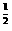 .
.
因为f(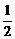 )=f(
)=f(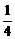 )·f(
)·f(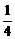 )=[f(
)=[f(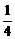 )]2,及f(
)]2,及f(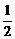 )=2
)=2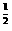 ,所以f(
,所以f(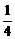 )=2
)=2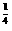 .
.
(2)证明:依题设y=f(x)关于直线x=1对称,故f(x)=f(1+1-x) f(x)=
f(x)=
f(2-x),x∈R.
又由f(x)是偶函数知f(-x)=f(x),x∈R,所以f(-x)=f(2-x),x∈R.将上式中-x以x代换,得f(x)=f(x+2),x∈R.
这表明f(x)是R上的周期函数,且2是它的一个周期.
20.(12分)(2003年北京)有三个新兴城镇,分别位于A、B、C三点处,且AB=AC=a,BC=2b.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处.(建立坐标系如下图)
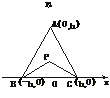
(1)若希望点P到三镇距离的平方和为最小,点P应位于何处?
(2)若希望点P到三镇的最远距离为最小,点P应位于何处?
分析:本小题主要考查函数、不等式等基本知识,考查运用数学知识分析问题和解决问题的能力.
(1)解:由题设可知,a>b>0,记h= ,设P的坐标为(0,y),则P至三镇距离的平方和为
,设P的坐标为(0,y),则P至三镇距离的平方和为
f(y)=2(b2+y2)+(h-y)2=3(y-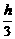 )2+
)2+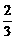 h2+2b2.
h2+2b2.
∴当y=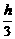 时,函数f(y)取得最小值.
时,函数f(y)取得最小值.
∴点P的坐标是(0,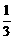
 ).
).
(2)解法一:P至三镇的最远距离为
g(y)=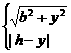
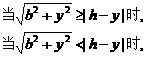
由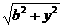 ≥|h-y|解得y≥
≥|h-y|解得y≥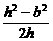 ,记y*=
,记y*=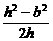 ,于是
,于是
g(y)=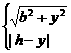
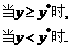
当y*=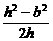 ≥0,即h≥b时,
≥0,即h≥b时,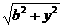 在[y*,+∞)上是增函数,而|h-y|在(-∞,y*)上是减函数,由此可知,当y=y*时,函数g(y)取得最小值;
在[y*,+∞)上是增函数,而|h-y|在(-∞,y*)上是减函数,由此可知,当y=y*时,函数g(y)取得最小值;
当y*=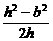 <0,即h<b时,函数
<0,即h<b时,函数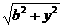 在[y*,+∞)上,当y=0时,取得最小值b,而|h-y|在(-∞,y*)上为减函数,且|h-y|>b.可见,当y=0时,函数g(y)取得最小值.
在[y*,+∞)上,当y=0时,取得最小值b,而|h-y|在(-∞,y*)上为减函数,且|h-y|>b.可见,当y=0时,函数g(y)取得最小值.
∴当h≥b时,点P的坐标为(0, );
);
当h<b时,点P的坐标为(0,0).其中h= .
.
解法二:P至三镇的最远距离为
g(y)=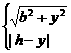
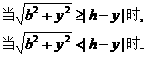
由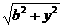 ≥|h-y|解得y≥
≥|h-y|解得y≥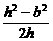 ,记y*=
,记y*=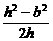 ,于是
,于是
g(y)=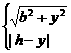
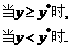
当y*≥0,即h≥b时,z=g(y)的图象如图(a),因此,当y=y*时,函数g(y)取得最小值.
当y*<0,即h<b时,z=g(y)的图象如图(b),因此,当y=0时,函数g(y)取得最小值.
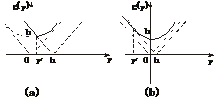
∴当h≥b时,点P的坐标为(0, );
);
当h<b时,点P的坐标为(0,0).其中h= .
.
解法三:∵在△ABC中,AB=AC=a,
∴△ABC的外心M在射线AO上,其坐标为(0, ),且AM=BM=CM.
),且AM=BM=CM.
当P在射线MA上,记P为P1;
当P在射线MA的反向延长线上,记P为P2.
若h= ≥b(如图(c)),
≥b(如图(c)),
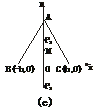
则点M在线段AO上.
这时P到A、B、C三点的最远距离为P1C或P2A,且P1C≥MC,P2A≥MA,
所以点P与外心M重合时,P到三镇的最远距离最小.
若h= <b(如图(d)),则点M在线段AO外.
<b(如图(d)),则点M在线段AO外.
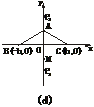
这时P到A、B、C三点的最远距离为P1C或P2A,且P1C≥OC,P2A≥OC,所以点P与BC边的中点O重合时,P到三镇的最远距离最小.
∴当 ≥b时,点P的位置在△ABC的外心(0,
≥b时,点P的位置在△ABC的外心(0, );
);
当 <b时,点P的位置在原点O.
<b时,点P的位置在原点O.
19.(12分)(2005年春季北京,理20)现有一组互不相同且从小到大排列的数据:a0,a1,a2,a3,a4,a5,其中a0=0.为提取反映数据间差异程度的某种指标,今对其进行如下加工:记T=a0+a1+…+a5,xn=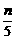 ,yn=
,yn=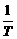 (a0+a1+…+an),作函数y=f(x),使其图象为逐点依次连结点Pn(xn,yn)(n=0,1,2,…,5)的折线.
(a0+a1+…+an),作函数y=f(x),使其图象为逐点依次连结点Pn(xn,yn)(n=0,1,2,…,5)的折线.
(1)求f(0)和f(5)的值;
(2)设Pn-1Pn的斜率为kn(n=1,2,3,4,5),判断k1、k2、k3、k4、k5的大小关系;
(3)证明f(xn)<xn(n=1,2,3,4).
(1)解:f(0)=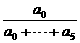 =0,
=0,
f(5)=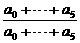 =1.
=1.
(2)解:kn=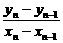 =
=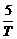 an,n=1,2,…,5.
an,n=1,2,…,5.
因为a1<a2<a3<a4<a5,
所以k1<k2<k3<k4<k5.
(3)证法一:对任何n(n=1,2,3,4),
5(a1+…+an)=[n+(5-n)](a1+…+an)
=n(a1+…+an)+(5-n)(a1+…+an)
≤n(a1+…+an)+(5-n)nan
=n[a1+…+an+(5-n)an]
<n(a1+…+an+an+1+…+a5)=nT,
所以f(xn)=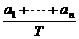 <
<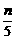 =xn.
=xn.
证法二:对任何n(n=1,2,3,4),
当kn<1时,
yn=(y1-y0)+(y2-y1)+…+(yn-yn-1)
=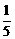 (k1+k2+…+kn)<
(k1+k2+…+kn)<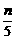 =xn.
=xn.
当kn≥1时,
yn=y5-(y5-yn)
=1-[(yn+1-yn)+(yn+2-yn+1)+…+(y5-y4)]
=1-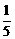 (kn+1+kn+2+…+k5)<1-
(kn+1+kn+2+…+k5)<1-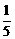 (5-n)=
(5-n)=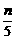 =xn,
=xn,
综上,f(xn)<xn.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com