
题目列表(包括答案和解析)
5、拟定从甲地到乙地通话 分钟的电话费由
分钟的电话费由 给出,其中
给出,其中 ,[m]是大于或等于
,[m]是大于或等于 的最小整数(如[3]=3,[3.7]=4, [3.1]=4),则从甲地到乙地通话时间为5.5分钟的话费为( ).
的最小整数(如[3]=3,[3.7]=4, [3.1]=4),则从甲地到乙地通话时间为5.5分钟的话费为( ).
|
A、3.71 |
B、3.97 |
C、4.24 |
D、4.77 |
4、函数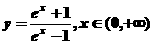 的反函数是( ).
的反函数是( ).
A、 |
B、 |
C、 |
D、 |
2、命题“p或q”是假命题,则下列判断正确的是( ).
|
A、命题“非p”与“非q”真假不同 |
B、命题“非p”与“非q”至多一个是真命题 |
|
C、命题“非p”或“非q”是假命题 |
D、命题“非p”且“非q”是真命题 |
3(理科)、如果不等式| |<1成立的充分非必要条件是
|<1成立的充分非必要条件是 ,则实数a的取值范围是( ).
,则实数a的取值范围是( ).
A、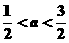 |
B、 |
C、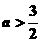 或 或 |
D、 或 或 |
(文科)、条件“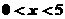 ”是条件“
”是条件“ ”的( )条件.
”的( )条件.
|
A、充分非必要 |
B、必要非充分 |
C、充要 |
D、非充分又非必要 |
1、设集合 ,
, ,若M∩N=Φ,则实数
,若M∩N=Φ,则实数 的取值范围是( ).
的取值范围是( ).
A、 |
B、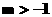 |
C、 |
D、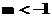 |
22.(本小题满分14分)F1、F2分别是椭圆 的左、右焦点,B是其上顶点,N是其右准线与x轴的交点,并且满足
的左、右焦点,B是其上顶点,N是其右准线与x轴的交点,并且满足 。
。
(1)求此椭圆的方程;
(2)若M是坐标平面内一动点,G是三角形MF1F2的重心,且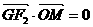 ,其中O是坐标原点,求动点M的轨迹C的方程;
,其中O是坐标原点,求动点M的轨迹C的方程;
(3)点P是此椭圆上一点,但非短轴端点,并且过P可作(2)中所求得轨迹C的两条不同的切线,Q、R是两个切点。
理科:求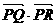 的最小值。
的最小值。
文科:当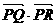 <0时,求点P 的横坐标的取值范围。
<0时,求点P 的横坐标的取值范围。
21.(本小题满分12分)
理科:已知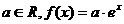 是定义在R上的单调递增函数,
是定义在R上的单调递增函数, 是它的反函数,并且曲线y=
是它的反函数,并且曲线y=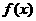 在其与坐标轴交点处的切线y=
在其与坐标轴交点处的切线y= 在其与坐标轴交点处的切线互相平行。
在其与坐标轴交点处的切线互相平行。
(1)求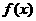 和
和 的解析式;
的解析式;
(2)设函数 ,当x>0且
,当x>0且 时,不等式
时,不等式 恒成立,求实数m的取值集合。
恒成立,求实数m的取值集合。
文料:设函数
(1)当 时,函数
时,函数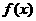 的图像经过点O(0,0)和M(1,1)两点,并且在原点处取极小值,求函数
的图像经过点O(0,0)和M(1,1)两点,并且在原点处取极小值,求函数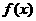 的极大值;
的极大值;
(2)求证:当函数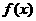 有极小值时,它也一定有极大值。
有极小值时,它也一定有极大值。
20.(本小题满分12分)已知数列 的各项均为正数,它的前n项和Sn满足
的各项均为正数,它的前n项和Sn满足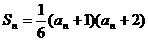 ,并且
,并且 成等比数列。
成等比数列。
(1)求数列 的通项公式;
的通项公式;
(2)理科:设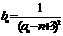 ,Tn是数列
,Tn是数列 的前n项和,求证:
的前n项和,求证: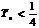 。
。
文科:设 ,Tn是数列
,Tn是数列 的前n项和,求证:
的前n项和,求证: 。
。
19.(本小题满分12分)甲、乙、丙三个口袋内都分别装有6个不相同的球,并且每个口袋内的6个球均有1个红球,2个黑球,3个无色透明的球,现从甲、乙、内三个口袋中依次随机各摸出1个球。
理科:(1)求恰好摸出红球、黑球和无色球各1个的概率;
(2)求摸出的3个球中含有有色球数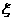 的概率分布列和数学期望。
的概率分布列和数学期望。
文科:(1)求恰好摸出2个黑球的概率;
(2)求恰好摸出红球、黑球和无色透明球各1个的概率;
(3)求摸出的3个球中至少有1个是有色球的概率。
17.(本小题满分12分)若A,B,C是三角形ABC的三个内角,向量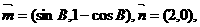 且
且 与
与 的夹角为
的夹角为 。
。
(1)求角B的大小;
(2)求 的取值范围。
的取值范围。
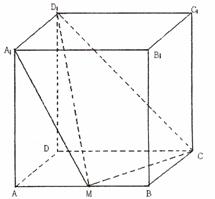 18.(本小题满分12分)在正方体ABCD-A1B1C1D1中,英才苑M是棱AB的中点
18.(本小题满分12分)在正方体ABCD-A1B1C1D1中,英才苑M是棱AB的中点
(1)求证:BC∥平面A1MD1;
(2)求二面角A1-D1M-C的大小。
16.设f(x)在其定义域R上是单调递增的奇函数, 在其定义域R上是偶函数,并且在区间
在其定义域R上是偶函数,并且在区间 上f(x)和
上f(x)和 的图像关于x轴对称,英才苑现在给出下列条件:
的图像关于x轴对称,英才苑现在给出下列条件:
① ②
② ③
③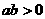 ④
④
其中能够使得不等式 恒成立的条件的序号是
恒成立的条件的序号是
(请把你认为正确的都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com