1．若且，则是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．第二象限角　 　　　　　　　　　　　　　　　　　 B．第一或第三象限角

C．第三象限角　 　　　　　　　　　　　　　　　　　 D．第二或第四象限角

22．(本小题满分14分)

已知上是增函数，在[0，2]上是减函数，且方程

有三个根，它们分别为.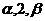

　　　 (Ⅰ)求c的值；

　　　 (Ⅱ)求证

　　　 (Ⅲ)求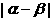的取值范围.

21．(本小题满分14分)

　 已知动点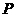与双曲线的两个焦点、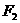的距离之和为定值，且

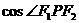的最小值为．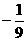

(I)求动点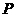的轨迹方程；

(II)若已知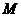，、在动点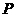的轨迹上且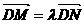，求实数的取值范围．

20．(本小题满分12分)

一片小树林有4000棵树，每年将砍伐20%的树木并种植1000棵树，设n年后所剩树木的棵数为，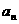

(I)计算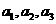的值；

(II)请猜想数列{a_n}的通项公式，并加以证明；

(III)试判断经过若干年后，树木的棵数能否大体稳定在某一固定值上？并说明理由.

19．(本小题满分12分)

一个电路中有三个电子元件，它们接通的概率都是m(0＜m＜1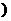如图，有如下三种联接方法：

①　　　　　　　　　　　　　　　 ②　　　　　　　　 ③

　 (I)分别求出这三种电路各自接通的概率；

　 (II)试分析这三种电路哪种性能最优，并证明你的结论.

18．(本小题满分12分)

　　 (甲)如图，已知直三棱柱中，是上的一个点,且.

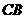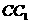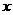　　　 (Ⅰ)分别以射线、、为轴、轴、

轴建立空间直角坐标系，求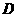点的坐标;

　　　 (Ⅱ)求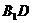与平面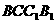所成的角的大小(用

反三角表示).

　　　 (乙)已知：如图，直三棱柱ABC-A₁B₁C₁中，AC⊥BC，AC=BC=CC₁，M、N分别为A₁B、B₁C₁的中点.

(Ⅰ)求证：MN//平面ACC₁

(Ⅱ)求证：MN⊥平面A₁BC；　　　　　　　　　　　　　　　　　　　　　

(Ⅲ)求二面角A-A₁B-C的大小.　　　　　　

17．(本小题满分12分)

　　　 在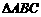中，内角A、B、C的对边分别为a、b、c，已知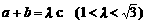，，求角A的取值范围.

注意：考生在(18甲)、(18乙)两题中选一题作答，如果两题都答，只以(18甲)计分.

16．一水池有2个进水口，1个出水口，进出水速度如图甲、乙所示.某天0点到6点，该水池的蓄水量如图丙所示。(至少打开一个水口)

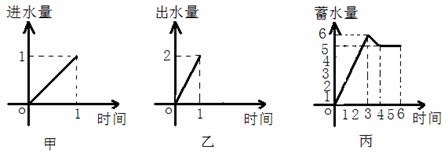
给出以下个论断：

　　 ①点到点只进水不出水；②点到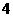点不进水只出水；③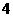点到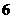点不进水不出水.

则一定不确定的论断是___________.

15．设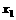、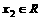,常数,定义运算,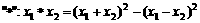

若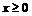,则动点的轨迹方程是__________________.

14．若圆锥的高为10cm，过顶点作与底面成45°的平面恰好把圆锥底面周长截去,则这截面的面积为　　　　　　　　　　　　　 　.