2.点P从(1，0)出发,沿单位圆 逆时针方向运动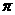弧长到达Q点,

则Q的坐标是

A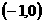．　　 B.(1，0) 　　　　C.　　　　 　D.(0，1)

一项是符合题目要求的.

1.已知集合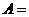{x|x＜5}，{1，2，3，4}，则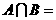

A.{1}　　　 B.{1，2}　　　 　　C.{1，2，3}　　 D.{1，2，3，4}

22.　 (本大题满分14分)设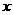、y∈R，i、j为直角坐标平面内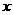、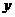轴正方向上的单位向量，向量a＝xi+(y+2)j，b＝xi+(y－2)j ，且| a |+| b |＝8． 　(1)求点M (x，y)的轨迹C的方程； 　(2)过点(0，3)作直线与曲线C交于A、B两点，设，是否存在这样的直线，使得四边形OAPB是矩形？若存在，求出直线的方程；若不存在，试说明理由．

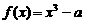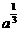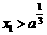21.　 (本大题满分12分) 已知a＞0，函数，x∈[0，+∞)，设x₁＞0，记曲线y＝f (x)在点M (x₁，f (x₁))处的切线为l． 　(1)求l的方程； 　(2)设l与x轴交点为(x₂，0)，证明：①x₂≥，②若，则．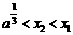

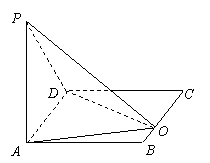
20.　 (本大题满分12分) 如图，在矩形ABCD中，AB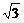＝，BC＝a，又PA⊥平面ABCD，PA＝4． 　　 (1)若在边BC上存在一点Q，使PQ⊥QD，求a的取值范围； 　(2)当BC上存在唯一点Q，使PQ⊥QD时，求异面直线AQ与PD所成角的大小； 　(3)若a＝4，且PQ⊥QD，求二面角A－PD－Q的大小．

19.　 (本大题满分12分)数列{a_n}是等比数列，a₁＝1，公比q是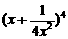的展开式中的第二项(按x的降幂排列)． 　(1)求数列{a_n}的通项a_n与前n项和S_n； 　(2)若，求A_n．

18.　 (本大题满分12分)在袋里装30个小球，其中彩球中有n (n≥2)个红色、5个蓝色、10个黄色，其余为白球．若从袋里取出3个都是相同颜色彩球(无白色)的概率是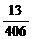，求红球的个数，并求从袋中任取3个小球至少有一个是红球的概率．

17.　 (本大题满分12分)已知向量a＝(cosx，sinx)，b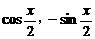＝()，且x∈[0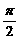，]．若f (x)＝a · b－2｜a+b｜的最小值是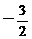，求的值．

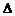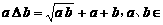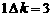16. 规定记号“”表示一种运算，即R^*．若，则函数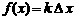的值域是　　　　　．

15. 某保险公司新开设了一项保险业务，规定该份保单在一年内如果事件E发生，则该公司要赔偿a元，假若在一年内E发生的概率为p，为使公司受益的期望值不低于a的，公司应要求该份保单的顾客缴纳的保险金最少为_________________元．