2．若α、β终边关于y轴对称，则下列等式成立的是　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A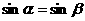．　　 B．　 C．　　 D．

　 3．设全集U=R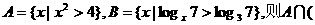，　 B)是　　　 (　　 )

　　　 A．　　　　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　　　　 D．

符合题目要求的)

1．给出下列函数：①，②，③，

　 ④，其中是偶函数的有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．1个　　　　　　　　　　 B．2个　　　　　　　　　　 C．3个　　　　　　　　　　 D．4个

22. 已知ΔOFQ的面积为2,且·=m .

(1)设＜m＜4,求向量与的夹角θ正切值的取值范围；

(2)设以O为中心，F为焦点的双曲线经过点Q(如图),||=c,m=(-1)c²,当||取得最小值时，求此双曲线的方程.(本题满分14分)

　 　黄冈市2005年秋期末调考试题

21.已知函数f(x)=log_ax(a>0且a≠1),若数列：2, f(a₁), f(a₂),…, f(a_n), 2n+4(n∈N^*)成等差数列.

(1)　 求数列{a_n}的通项a_n；

(2)　 若0<a<1，数列{a_n}的前n项和为S_n,求S_n；

(3)　 若a=2，令b_n=a_n·f(a_n)，试比较b_n+1与b_n的大小.(本题满分12分)

20.若函数y=f(x)是周期为2的偶函数,当x∈[2,3]时,f(x)=x-1,在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中2＜a＜3),求△ABC面积的最大值.(本题满分12分)

19.某学生语文、数学、英语三科考试成绩，在本次调研考试中排名全班第一的概率:语文为0.9，数学为0.8，英语为0.85，问这次考试中

　 (1)该生三科成绩均未获得第一名的概率是多少？

(2)该生恰有一科成绩未获得第一名的概率是多少? (本题满分12分)

18. (1)已知||=4，||=3，(2－3)·(2+)=61，求与的夹角θ；

　　 (2)设=(2，5)，=(3，1)，=(6，3)，在上是否存在点M，使

　 　⊥，若存在，求出点M的坐标，若不存在，请说明理由. (本题满分12分)

17.已知向量=(sinB，1－cosB)，且与向量=(2，0)所成角为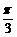，其中A, B, C是△ABC的内角．　 (1)求角B的大小；　

(2)求sinA+sinC的取值范围．((本题满分12分))

16.设函数f(x)=x|x|+bx+c,给出下列命题：

　　　 ①b=0, c>0 时，方程f(x)=0只有一个实数根；②c=0时，y=f(x)是奇函数；

　　　 ③y=f(x)的图象关于点(0，c)对称；④方程f(x)=0至多有两个实根.

　　 上述四个命题中所有的正确命题的序号为　　　　　 　.

15.若双曲线的一条准线恰为圆x²+y²+2x=0的一条切线,则k等于_____.