
题目列表(包括答案和解析)
6. 某公司有N个员工,下设若干部门,现采用分层抽样方法从全体员工中抽取一个容量为n的样本(N是n的正整数倍)。已知某部门被抽取了m个员工,则这一部门的员工数为
A.
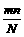 B.
B. 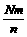 C.
C.
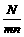 D.
D.
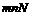
5. 命题“若a,b都是奇数,则a+b是偶数”的逆否命题是
A. 若a+b不是偶数,则a,b都不是奇数
B . 若a+b不是偶数,则a,b不都是奇数
C. 若a+b是偶数,则a,b都是奇数
D. 若a+b是偶数,则a,b不都是奇数
4. 函数 的单调递增区是
的单调递增区是
A.  B.(0,+∞) C.
B.(0,+∞) C. 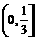 D.
D. 
3. 与函数 有相同图象的一个函数是
有相同图象的一个函数是
A.
 B.
B.
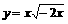
C.
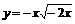 D.
D.
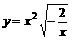
2. “m>1,n>1”是“logmn>0”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
1. 如果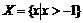 ,那么
,那么
A.
 B.
B.
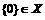 C.
C.
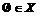 D.
D.
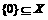
22、解:由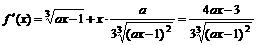 ,……………………4分
,……………………4分
令 即
即 ,得
,得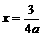 。…………………………5分
。…………………………5分
又当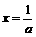 时函数
时函数 的导数不存在。…………………………6分
的导数不存在。…………………………6分
当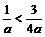 即
即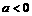 时,由下表
时,由下表
|
x |
 |
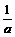 |
 |
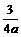 |
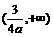 |
 |
+ |
不存在 |
+ |
0 |
- |
 |
↗ |
0 |
↗ |
 |
↘ |
∴ 的单调递增区间为
的单调递增区间为 ,
, ,递减区间为
,递减区间为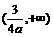 ,
,
当x=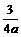 时
时 有极大值
有极大值
 。………………………………9分
。………………………………9分
当 即
即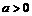 时,由下表
时,由下表
|
x |
 |
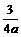 |
 |
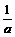 |
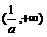 |
 |
- |
0 |
+ |
不存在 |
+ |
 |
↘ |
 |
↗ |
0 |
↗ |
∴ 的单调递增区间为
的单调递增区间为 ,
,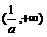 ,递减区间为
,递减区间为 ,当x=
,当x=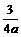 时
时 有极小值
有极小值
 。
。
∴综上所述,当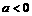 时,原函数的递增区间为
时,原函数的递增区间为 ,
, ,递减区间为
,递减区间为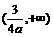 ,有极大值
,有极大值 ;当
;当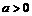 时,原函数的递增区间为
时,原函数的递增区间为 ,
,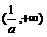 ,递减区间为
,递减区间为 ,有极小值
,有极小值 。…………………………12分
。…………………………12分
21、解:(1)∵ 对任意x,y都有
对任意x,y都有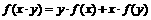 ,
,
∴令x=y=1时,有 ,
,
∴f (1)=0…………………………………………2分
∴令x=y=-1时,有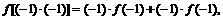 ,
,
∴f (-1)=0。…………………………………………5分
(2)∵f(x)对任意x,y都有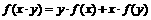
∴令x=t,y=-1,有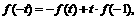
将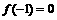 代入得
代入得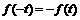 ,
,
∴函数 是
是 上的奇函数。……………………8分
上的奇函数。……………………8分
(3)①当n=1时,左边=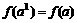 ,右边=
,右边=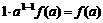 ,等式成立。
,等式成立。
当n=2时,左边=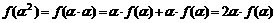 ,
,
右边=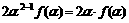 ,等式成立…………………………10分
,等式成立…………………………10分
② 假设当n=k时,等式成立,即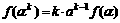
则当n=k+1时,有
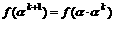
=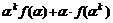
=
=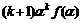 。
。
表明当n=k+1时等式也成立。
综上①②,对任意正整数,等式 成立…………………………14分
成立…………………………14分
20、(1)解:∵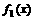 的值域为
的值域为 ,∴
,∴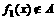 ………………2分
………………2分
对于 ,定义域为
,定义域为 ,满足条件①。
,满足条件①。
而由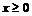 知
知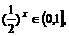 ∴
∴ ,满足条件②
,满足条件②
又∵ ,∴
,∴ 在
在 上是减函数。
上是减函数。
∴ 在
在 上是增函数,满足条件③
上是增函数,满足条件③
∴ 属于集合A。……………………………………6分
属于集合A。……………………………………6分
(2)由(1)知,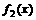 属于集合A。
属于集合A。
∴原不等式为 ………………8分
………………8分
整理为: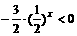 。…………………………10分
。…………………………10分
∵对任意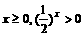 ,
,
∴原不等式对任意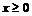 总成立……………………12分
总成立……………………12分
19、解:∵ 在定义域
在定义域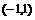 内可导并满足
内可导并满足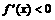 ,
,
∴ 在
在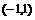 内是减函数。……………………3分
内是减函数。……………………3分
∴由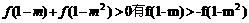
∴由 是奇函数得
是奇函数得 ……………………6分
……………………6分
∴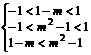 …………………………10分
…………………………10分
∴ 。
。
∴原不等式的解集为(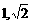 )……………………12分
)……………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com