
题目列表(包括答案和解析)
4.归纳小结
在以上学习的基础上,师生共同归纳小结:复数加减法的运算法则,要求学生能够熟练地运用文字语言或符号语言表达这一法则。
3.规定负数的减法是加法的逆运算,即把满足
(C+di)+(x+yi)=a+bi
的复数x+yi,叫做复数a+bi减去c+di的差。教学中,由学生自己计算出结果。
2. 引导学生验证,复数的加法满足交换率、结合率,及对任意z1 、z2、 z3 C,有
C,有
Z1+Z2=Z2+Z1,
(Z1+Z2)+Z3=Z1+(Z2+Z3).
1. 提出复数的加法法则:(a+bi)+(c+di)=(a+c)+(b+d)i.
2. 理解复数的加法、减法的几何意义,会用向量法则来进行复数的加法与减法运算教学过程
1. 掌握复数代数形式的加法与减法运算法则,能够熟练地进行复数代数形式的加法与减法运算。
19 (本小题满分12分)设函数
(本小题满分12分)设函数 ,求使f(x)≥2
,求使f(x)≥2 的x取值范围
的x取值范围
20 (本小题满分12分)已知△ABC的面积S满足
(本小题满分12分)已知△ABC的面积S满足 , 且
, 且 ,
,  与
与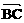 的夹角为
的夹角为

(I) 求 的取值范围;
的取值范围;
(II)求函数 的最小值
的最小值
21 (本小题满分14分)某公司生产的A型商品通过租赁柜台进入某商场销售,第一年商场为吸引厂家,决定免收该年的管理费,因此,该年A型商品定价为每件70元,销售量为11
(本小题满分14分)某公司生产的A型商品通过租赁柜台进入某商场销售,第一年商场为吸引厂家,决定免收该年的管理费,因此,该年A型商品定价为每件70元,销售量为11 8万件;第二年商场开始对该商品征收比率为p%的管理费(即每销售100元要征收p元),于是该商品的定价上升为每件
8万件;第二年商场开始对该商品征收比率为p%的管理费(即每销售100元要征收p元),于是该商品的定价上升为每件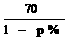 元,预计年销售量将减少p万件
元,预计年销售量将减少p万件
(Ⅰ)将第二年商场对商品征收的管理费y万元表示成p的函数,并指出这个函数的定义域;
(Ⅱ)要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征收管理费的比率p%的范围是多少?
(Ⅲ)第二年,商场在所收管理费不少于14万元的前提下,要让厂家获得最大销售额,则p应为多少?
22 (本小题满分14分)设
(本小题满分14分)设 是定义域为
是定义域为 的奇函数,且它在区间
的奇函数,且它在区间 上是增函数
上是增函数
(I)用定义证明 在区间
在区间 上是增函数;
上是增函数;
(II) 若 ,解关于
,解关于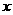 的不等式:
的不等式:
 (其中
(其中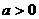 且
且 )
)
23 (本题满分14分) 对于函数
(本题满分14分) 对于函数 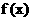 ,若存在
,若存在 ,使
,使  成立,
成立,
则称 为
为 的“滞点”
的“滞点” 已知函数f ( x ) =
已知函数f ( x ) = 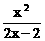

(I)试问 有无“滞点”?若有,求之,否则说明理由;
有无“滞点”?若有,求之,否则说明理由;
(II)已知数列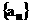 的各项均为负数,且满足
的各项均为负数,且满足 ,求数列
,求数列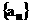 的通项公式;
的通项公式;
(III)已知 ,求
,求 的前项和
的前项和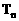

2005-2006学年度高三年级第一学期11月份调研考试
13 在
在 和
和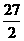 之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为___▲____.
之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为___▲____.
14 已知向量
已知向量 不超过5,则k的取值范围是 ▲
不超过5,则k的取值范围是 ▲ 
15 已知
已知 、
、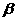 均为锐角,且
均为锐角,且 = ▲
= ▲ 
16 若正整数m满足
若正整数m满足 ,则m
= ▲
,则m
= ▲ 

17.若函数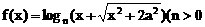 ,
,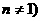 是奇函数,则a= ▲
是奇函数,则a= ▲ 
18
 是正实数,设
是正实数,设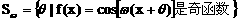 ,若对每个实数
,若对每个实数 ,
, 的元素不超过2个,且有
的元素不超过2个,且有 使
使 含2个元素,则
含2个元素,则 的取值范围是___▲ ___
的取值范围是___▲ ___
1 若非空数集A = {x|2a + 1≤x≤3a-5 },B = {x|3≤x≤22 },则能使
若非空数集A = {x|2a + 1≤x≤3a-5 },B = {x|3≤x≤22 },则能使 成立的所有a的集合是
A.{a|1≤a≤9} B.{a|6≤a≤9} C.{a|a≤9} D.
成立的所有a的集合是
A.{a|1≤a≤9} B.{a|6≤a≤9} C.{a|a≤9} D.
2 已知二个不共线向量
已知二个不共线向量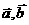 ,且
,且 则一定共线的三点是
则一定共线的三点是
A A、B、D B
A、B、D B A、B、C C
A、B、C C B、C、D D
B、C、D D A、C、D
A、C、D
3 已知函数
已知函数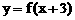 是偶函数, 则函数
是偶函数, 则函数 图象的对称轴为直线
图象的对称轴为直线
A
 B
B
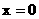 C
C
 D
D

4 从原点向圆 x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为
从原点向圆 x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为
A π
B
π
B 2π
C
2π
C 4π
D
4π
D 6π
6π
5 命题p:若a、b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件;命题q:函数
命题p:若a、b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件;命题q:函数
y= 的定义域是(-∞,-1
的定义域是(-∞,-1 ∪[3,+∞
∪[3,+∞ ,则
,则
A “p或q”为假 B
“p或q”为假 B “p且q”为真 C
“p且q”为真 C p真q假 D
p真q假 D p假q真
p假q真
6 若x,y是正数,则
若x,y是正数,则 的最小值是
的最小值是
A.3 B. C.4 D.
C.4 D.
7 在R上定义运算
在R上定义运算 :
: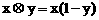
 若不等式
若不等式 对任意实数
对任意实数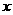 成立,则
成立,则
A. B.
B. C.
C. D.
D.
8 已知k<-4,则函数y=cos2x+k(cosx-1)的最小值是
已知k<-4,则函数y=cos2x+k(cosx-1)的最小值是
(A) 1 (B) -1 (C) 2k+1 (D) -2k+1
9 设函数
设函数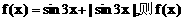 为
为
A.周期函数,最小正周期为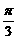 B.周期函数,最小正周期为
B.周期函数,最小正周期为
C.周期函数,最小正周期为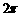 D.非周期函数
D.非周期函数
10 锐角三角形ABC中,a、b、c分别是三内角A、B、C的对边
锐角三角形ABC中,a、b、c分别是三内角A、B、C的对边 设B=2A,则
设B=2A,则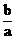 的取值范围是
的取值范围是
A.(-2,2) B.(0,2) C.( ,2) D.(
,2) D.(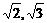 )
)
11 设
设 是函数
是函数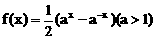 的反函数,则使
的反函数,则使 成立的
成立的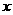 的取值范围为
的取值范围为
A
 B
B
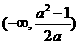 C
C
 D
D

12.经济学中的“蛛网理论”(如图),假定某种商品的“需求-价格”函数的图象为直线l1,“供给-价格”函数的图象为直线l2,它们的斜率分别为k1、k2,l1与l2的交点P为“供给-需求”均衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点P,与直线l1、 l2的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点P的条件为

A k1+k2>0 B
k1+k2>0 B k1+k2=0 C
k1+k2=0 C k1+k2<0 D
k1+k2<0 D k1+k2可取任意实数
k1+k2可取任意实数
22.(14分)点 为曲线
为曲线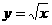 上横坐标为n的点,过点An作曲线的切线
上横坐标为n的点,过点An作曲线的切线 与x
与x
轴交于点Bn,设△OAnBn的面积为an(O为原点).
(1)求an;
(2)设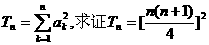 ;
;
(3)求 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com