
题目列表(包括答案和解析)
2、 填空
① 若不等式(a-2)x2+2(a-2)x-4<0对一切实数x都成立,
则a的取值范围是
② 若不等式(m2+4m-5)x2-4(m-1)x+3>0对一切实数x恒成立,
则m的取值范围是
③ 函数y=2x2-mx+3,当x∈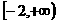 时是增函数,则m的取值范围是
时是增函数,则m的取值范围是
④ 若x,y∈R+且xy-(x+y)=1,则x+y的最小值是
⑤不等式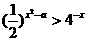 的解集是(-2,4),则实数a的值为
的解集是(-2,4),则实数a的值为
⑥若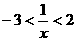 的解集是
,|x-1|+|x-2|>3的解集是
的解集是
,|x-1|+|x-2|>3的解集是
2<|x+1|≤5 的解集是
⑦若不等式|x-2|+ |x+1|<a的解集不是空集,则a∈
|x-2|-|x+1|>a的解集是空集,则a∈
⑧若x1,x2是关于x的方程7x2-(k+13)x+k2-k-2=0的两根,且0<x1<1<x2<2,求k的范围
⑨f(x)是关于x的一次函数,若1≤f(1)≤2,3≤f(2)≤4,则f(3)的取值范围是
⑩已知关于x的不等式ax2+bx+c<0的解集为{x|x<α或x>β}其中α<β<0,
那么不等式cx2-bx+a>0的解集是
⑾不等式 的解集为
的解集为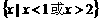 ,那么
,那么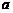 的值等于___ 答案
的值等于___ 答案
(1)理解不等式的性质及其证明。 (2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用。 (3)掌握分析法、综合法、比较法证明简单的不等式。 (4)掌握简单不等式的解法。 (5)理解不等式 |a|-|b|≤|a+b|≤|a|+|b|。 二、再现性题组
1、 选择
①不等式 ≥0的解集是
( )
≥0的解集是
( )
A.{x| x<-2或x>2} B.{x| x<-2或-1≤x≤1或x>2}
C.{x| x<-2或x≥1} D.{x| x≤-1或x>2}
②若log a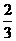 <1,则
( )
<1,则
( )
A.0<a<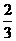
 B.
B.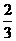 <a<1 C.0<a<
<a<1 C.0<a<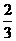 或a>1 D.a>
或a>1 D.a>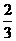
③若a>0,b>0,则不等式a>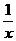 >-b的解集为
( )
>-b的解集为
( )
A. B.
B.
C.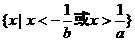 D.
D.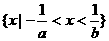
④已知:M={x|3-x≥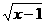 },N={x|x2-(a+1)x+a≤0},当M
},N={x|x2-(a+1)x+a≤0},当M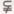 N时a的取值范围是( )
N时a的取值范围是( )
A.a≥1 B.1<a<2 C.a>2 D.a≥2
⑤若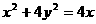 ,则S=x2+y2有
( )
,则S=x2+y2有
( )
A. 最小值0,最大值16 B.
最小值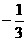 ,最大值4
,最大值4
C. 最小值0,最大值1 D. 最小值1,最大值16
⑥若不等式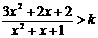 ,对x∈R恒成立,则正整数k的值为
( )
,对x∈R恒成立,则正整数k的值为
( )
A.1 B.2 C.3 D.4
4. 课堂小结
由y=f(u) ,u=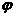 (x)可得复合函数y=f
(x)可得复合函数y=f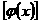 .
.
关于复合函数的导数,要理解法则,掌握步骤,善于应用.
(1)
法则 y' = y'
= y'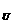 ·u'
·u'
(2) 步骤 分解---求导---回代(熟练后可省写步骤)
(3) 应用 能对复合函数求导;能解有关的应用问题
布置作业
教科书习题3 , 4 第2 (3) (4) , 3题.
研究题 已知曲线y=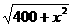 +
+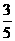 (100-x) (0
(100-x) (0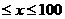 ) 在点M 处有水平切线,求点M的坐标.
) 在点M 处有水平切线,求点M的坐标.
略解: 易得
y'=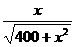 _
_ 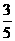 .
.
令y'=0 ,解得x=15 .
点M 的坐标是(15 ,76) .
3.反馈练习
学生完成教科书练习第1 , 2题
3. 应用求导法则
(1)应用之一:对复合函数式求导
例2 求下列函数的导数:
(1)
y=
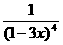 ; (2)y=sinx
; (2)y=sinx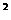 ; (3)y=cos(3x-
; (3)y=cos(3x- ); (4)y=
); (4)y=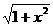
请学生上台完成.
答案:(1)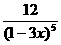 ; (2)2xcosx
; (2)2xcosx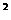 ; (3)-3sin(3x-
; (3)-3sin(3x- ); (4)
); (4)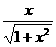
注:这里有分式型,根式型,三角函数型的复合函数求导.
师生一起评议.可表扬四位学生完成得较好.接着提请注意,熟练后可省写步骤,并作示范.
如,解(1)可表达为y
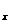 =
=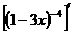 =-4(1-3x)
=-4(1-3x)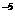 .(-3)=12(1-3x)
.(-3)=12(1-3x)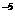 这里最后结果可写负指数或分数指数。
这里最后结果可写负指数或分数指数。
出示教科书例3并讲解。
其中对u=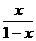 求u
求u
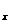 ,可让学生在草稿上完成。此处,教师可作如下指导:
,可让学生在草稿上完成。此处,教师可作如下指导:
方法一 按商的求导法则求导。
方法二 先化为u=-1+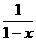 ,即u=-1+v
,即u=-1+v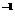 ,v=1-x,按复合函数求导。
,v=1-x,按复合函数求导。
(2)应用之二 解简单的应用问题
增例
当n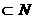 *时,求证:C
*时,求证:C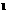
 +2C
+2C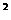
 +
+ C
C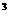
 +……+nC
+……+nC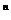
 =n2
=n2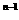 .
.
引导学生分析,联想到二项展开式(1+x)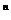 =C
=C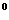
 +C
+C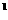
 X+C
X+C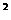
 X
X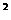 +……+C
+……+C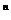
 X
X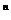 .(*)
.(*)
对比展开式通项C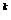
 x
x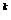 与待证和式通项kC
与待证和式通项kC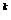
 ,可决定对(*)式求导并赋值x=1证得.
,可决定对(*)式求导并赋值x=1证得.
视学生水平由教师讲解或学生完全证明.
证明:由(1+x)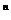 =C
=C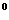
 +C
+C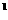
 x+C
x+C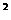
 x
x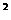 +……+C
+……+C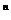
 x
x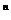 ,
,
两边对x求导,得
n(1+x)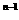 ﹒1=0+C
﹒1=0+C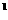
 +2
+2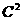
 x+……+nC
x+……+nC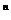
 x
x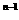 ,
,
令x=1,得
n﹒2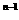 =C
=C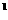
 +2C
+2C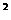
 +……+nC
+……+nC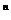
 .
.
注:应向学生讲清(1+x)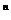 是作为复合函数对x求导的.
是作为复合函数对x求导的.
对此题在思考.在<<排列,组合和概率>>一章中,我们用的证法是倒序相加法,通项变换法,不妨重温一下.
方法一 倒序相加法
令S =C
=C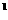
 +2C
+2C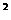
 +……+(n-1) n
+……+(n-1) n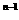
 +n C
+n C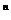

(1)式右边倒序,写为
 =n
=n +(n-1)
+(n-1)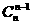 +(n-2)
+(n-2)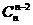 +……+
+……+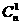
注意到组合数性质 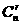 =
=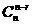 (r=1,2,3,……,n)
(r=1,2,3,……,n)
(2) 式可改写为
 =n
=n +(n-1)
+(n-1)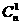 +(n-2)
+(n-2)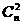 +……+
+……+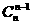
将(1)﹑(3)两式相加(注意错位)得
2 =n(
=n( +
+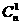 +
+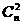 +……+
+……+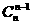 +
+ )
)
即2S =n2
=n2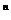
S =n2
=n2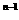
即C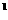
 +2 C
+2 C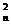 +……+n C
+……+n C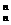 =n2
=n2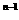
方法二 通项变化法
k =k
=k
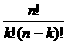 =n
=n
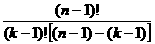 =n
=n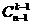
即 k =n
=n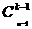
在这一等式中顺次取k=1,2……,n,并相加得
C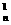 +2 C
+2 C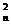 +…… +n C
+…… +n C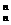 =n C
=n C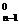 +n C
+n C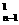 +……+n C
+……+n C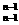
=n (C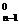 + C
+ C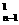 +…… + C
+…… + C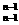 )
)
=n 2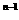
1.复合求导法则
让学生回答复合函数定义,求导法则,求导步骤.
本节将在应用中熟练掌握复合函数的求导.
2. 会用复合函数的求导法则解决一些简单的问题.
教学过程:
1. 掌握复合函数的求导法则.
6.讲解例3、例4
例3 实数x分别取什么值时,复数
z二x2+x一6+(x2-2x一15)i
是(1)实数?(2)虚数?(3)纯虚数?(4)零?
分析:因为x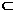 R,所以x2+x一6,x2-2x-15都是实数,由复数:’。+航是实数虚数、纯虚数与零的条件可以确定实数x的值,
R,所以x2+x一6,x2-2x-15都是实数,由复数:’。+航是实数虚数、纯虚数与零的条件可以确定实数x的值,
解:(1)当x2-2x一15二0,即x二一3或x二5时
(2)当x2-2x-15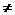 0,即x
0,即x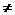 -3且x
-3且x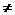 5
5
(3)当x2+x一6=0且x2-2x一15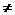 0,即x=2
0,即x=2
(4)当x2+x一6=0且x2-2x一15=0,即x=-3
例4 求适合下列方程中的z与y(x、y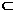 R)的值.
R)的值.
(1)x2十2+(x一3)I=y2+9十(y-2)i
(2)2x2-5x十3+(y2+y一6)I=0.
分析:因为x,y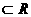 ,所以由两个复数相等的定义个方程组,可求出z,9的值
,所以由两个复数相等的定义个方程组,可求出z,9的值
解:(1)根据复数相等的定义
x2十2二y2十9,
x-3=y-2.
所以, x=4,y=3.
得方程组
(2)根据复数相等的定义,得方程组
2x2-5x十3=0,

y2十y-6=0.
X=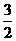 ,或x=1
,或x=1
Y=-3,或y=2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com