
题目列表(包括答案和解析)
8.若复数 为虚数单位)是纯虚数,则实数a的值为 ( )
为虚数单位)是纯虚数,则实数a的值为 ( )
A.-2 B.4 C.-6 D.6
7.若函数f(x)是定义在R上的偶函数,在 上是减函数,且f(2)=0,则使得f(x)<0的x
上是减函数,且f(2)=0,则使得f(x)<0的x
的取值范围是 ( )
A.(-∞,2) B.(2,+∞)
C.(-∞,-2)∪(2,+∞) D.(-2,2)
6.“m=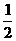 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( )
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( )
A.充分必要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
5.计算机中常用十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符
号,这些符号与十进制的数的对应关系如下表:
|
十六进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
十进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
例如:用十六进制表示:E+D=1B,则A×B=
A.6E B.72 C.5F D.B0
4. = ( )
= ( )
A.-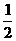 B.
B.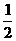 C.-
C.-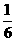 D.
D.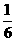
3.函数 反函数是 ( )
反函数是 ( )
A.y=1+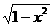 (-1≤x≤1) B.y=1+
(-1≤x≤1) B.y=1+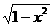 (0≤x≤1)
(0≤x≤1)
C.y=1-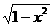 (-1≤x≤1) D.y=1-
(-1≤x≤1) D.y=1-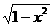 (0≤x≤1)
(0≤x≤1)
2.映射f:A→B,如果满足集合B中的任意一个元素在A中都有原象,则称为“满射” 已
已
知A中有4个元素,B中有3个元素,那么从A到B的不同满射的个数为 ( )
A.24 B.6 C.36 D.72
1.设I为全集,S1 S2
S2 S3是I的三个非空子集,且S1∪S2∪S3=I,则下面论断正确的是( )
S3是I的三个非空子集,且S1∪S2∪S3=I,则下面论断正确的是( )
A.C1S1∩(S2∪S3)=φ B.S1 (C1S2∩C1S3)
(C1S2∩C1S3)
C.C1S1∩C1S2∩C1S3=φ D.S1 (C1S2∪C1S3)
(C1S2∪C1S3)
(17) 由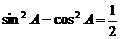 ,得
,得 .
.
∵DABC是锐角三角形,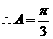 . …………………………..3分
. …………………………..3分
设DABC外接圆半径为R(R>0),由正弦定理得
 ………..9分
………..9分
若B=C,则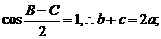
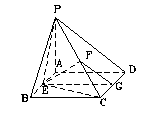 若B¹C,则
若B¹C,则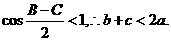 ………………………..12分
………………………..12分
(18)证(Ⅰ)∵PA^底面ABCD
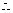 AD是PD在平面ABCD内的射影。
AD是PD在平面ABCD内的射影。
∵CDÌ平面ABCD,且CD^AD,
故CD^PD .………………...…4分
(Ⅱ)取CD中点G,连结EG、FG
∵E、F分别是AB、PC的中点,\EG//AD,FG//PD,
\平面EFG//平面PAD,\EF//平面PAD. ……………..……8分
(Ⅲ)当平面PCD与平面ABCD成45°角时,直线EF^平面PCD。
证明:G为CD中点,则EG^CD,由(1)知FG^CD,
故ÐEGF为平面PCD 与平面ABCD所成二面角的平面角,即ÐEGF=45°,
从而得ÐADP=45°, AD=AP。
由RtDPAE@RtDCBE,得PE=CE。
又F是PC的中点,\EF^PC。
由CD^EG,CD^FG,得CD^平面EFG,CD^EF,即EF^CD,
故EF^平面PCD. …………..……………….………….12分
(19)(Ⅰ) 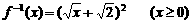 .…………………………..4分
.…………………………..4分
(Ⅱ) ∵
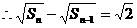
则 是首项为
是首项为 、公差为
、公差为 的等差数列,
的等差数列,
故 ,由
,由 ,可求得
,可求得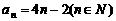 .…8分
.…8分
(Ⅲ) 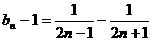 ,
,
则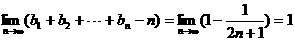 .………….12分
.………….12分
(20) ( I )到第 年该公司共有
年该公司共有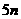 名职工,基础工资总额为
名职工,基础工资总额为 万元,
万元,
房屋补贴总额为: …..2分
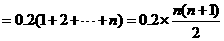
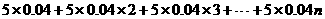
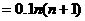 万元, ……….……………………..4分
万元, ……….……………………..4分
医疗费总额为 (万元)
(万元)
 …………6分
…………6分
 (II)
(II)
∴每年房屋补贴和医疗费用的总和不会超过基础工资总额20%. …..….12分
(21)(1)以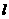 为
为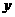 轴,且点
轴,且点 在
在 轴的正半轴上建立直角坐标系,则
轴的正半轴上建立直角坐标系,则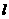 的方程为
的方程为 ,
,
点 的坐标为
的坐标为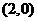 ,设点
,设点 是曲线段
是曲线段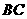 上任意一点,则
上任意一点,则
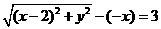 ,
,
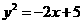
 .………..4分
.………..4分
(2)设点
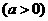 ,点
,点 是曲线段
是曲线段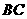 上任意一点,依题意:
上任意一点,依题意:


 ,…….6分
,…….6分
若 即
即 ,则当
,则当 时,
时, ;………..8分
;………..8分
若 即
即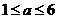 ,则当
,则当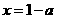 时,
时, ;……….10分
;……….10分
若 即
即 ,则当
,则当 时,
时, .………..12分
.………..12分
(22)
(Ⅰ)  ,
……….……2分
,
……….……2分
设  ,
,

故 . ……………….………..6分
. ……………….………..6分
又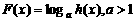 ,
,
 从而
从而
又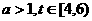 ,
,
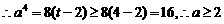 ,等号在t=4, x=0时取得.….……….8分
,等号在t=4, x=0时取得.….……….8分
(Ⅱ) 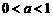 时,
时,

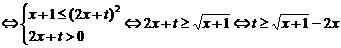 .
.
若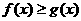 恒成立,只要
恒成立,只要 恒成立,
恒成立,
即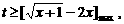 …………………11分
…………………11分
令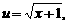 则
则
故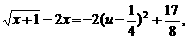 当u=1时,
当u=1时, ,
,
即所求t的范围是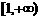 .…………………………..………….14分
.…………………………..………….14分
(13) (14)
(14) 或-2
(15)
或-2
(15) (16)540
(16)540
提示:(14)由 ,得
,得 ,可解.
,可解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com