
题目列表(包括答案和解析)
22、(本题满分14分)
已知函数f (x) = ln (2-x) + ax在(0,1)上是增函数;
(Ⅰ)求实数a的取值范围;
(Ⅱ)若数列{an}满足:a1 Î(0,1),an+1 = ln(2-an)+an(nÎN*),
证明:0< an < an+1 <1;
(Ⅲ)若数列{bn}满足:b1 Î(0,1),bn+1 = 2ln(2-bn)+bn(nÎN*),问数列{bn}是否具有单调性?若有单调性,请给出证明,若不存在单调性,请说明理由。
21、(本题满分12分)
甲、乙两人掷硬币,甲用一枚硬币掷3次,记下国徽面朝上的次数为m;乙用一枚硬币掷2次,记下国徽面朝上的次数为n
(1)计算国徽面朝上不同次数的概率并填入下表:
|
国徽面朝上次数m |
3 |
2 |
1 |
0 |
||
|
P(m) |
|
|
|
|
||
|
国徽面朝上次数n |
2 |
1 |
0 |
|||
|
P(n) |
|
|
|
|||
(2)现规定:若m > n,则甲胜;若n ³ m,则乙胜。你认为这种规定合理吗?,为什么?
20、(本题满分12分)
(1)已知a,b是正常数,且a ¹ b, x、y Î(0,+¥),求证: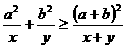 ,指出等号成立的条件;
,指出等号成立的条件;
(2)利用(1)的结论,求函数 的最小值,并指出f(x)取最小值时x的值。
的最小值,并指出f(x)取最小值时x的值。
19、(本题满分12分)
已知等差数列{an}的首项 a1=1,公差d>0,且第二项,第五项,第十四项分别是等比数列{bn}的第二项、第三项、第四项.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设数列{cn}对任意的n∈N*,均有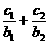 +…+
+…+ =an+1成立,
=an+1成立,
求c1+c2+…+c2006 的值.
18、(本题满分12分)
已知a = (cos2x,sin2x), b = (cosx,-sinx), c = ( ,-1),其中
,-1),其中 ;
;
(1)当a∥b时,求x的值的集合;
(2)设f(x) = |a - c|2,求f(x)的单调递增区间。
17、(本题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c,且a+c=10,C=2A, 。
。
求:(1) 的值;(2)b的值。
的值;(2)b的值。
16、 如图,一单位正方体形积木,平放与桌面上,在其上放置若干个小正方体形积木摆成塔形,其中上面正方体中下底的四个顶点是下面相邻正方体中上底面各边的中点,如果所有正方体暴露在外面部分的面积和超过8.8,则正方体的个数是
.
如图,一单位正方体形积木,平放与桌面上,在其上放置若干个小正方体形积木摆成塔形,其中上面正方体中下底的四个顶点是下面相邻正方体中上底面各边的中点,如果所有正方体暴露在外面部分的面积和超过8.8,则正方体的个数是
.
15、 如图,函数y=f(x)的图像在点P处的切线方程是
如图,函数y=f(x)的图像在点P处的切线方程是
14、定义R在上的函数 为奇函数,则
为奇函数,则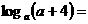
13、若 的展开式中的第四项是10a2(a为大于0的常数),则x=
;
的展开式中的第四项是10a2(a为大于0的常数),则x=
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com