1、在复平面内，复数(为虚数单位)所对应的点位于 (　　 )　　　　　　　　　　　　　　

A．第一象限　　B.第二象限　　　　 C．第三象限　　D.第四象限

22.(本小题满分14分)已知a≥，f(x)=－a²x²+ax+c.

(1)证明对任意x∈［0，1］，f(x)≤1的充要条件是c≤;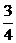

(2)已知关于x的二次方程f(x)=0有两个实根α、β，证明：|α|≤1且|β|≤1的充要条件是c≤a²－a.

21.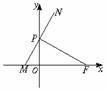(本小题满分12分)如图，点F(a，0)(a>0)，点P在y轴上运动，M在x轴上，N为动点，且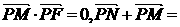0.

(1)求点N的轨迹C的方程；

(2)过点F(a，0)的直线l(不与x轴垂直)与曲线C交于A、B两点，设点K(－a，0)，与的夹角为θ，求证：0<θ<.

20.(本小题满分12分)如图，已知正三棱柱ABC-A₁B₁C₁中，过BC₁的平面BC₁D∥AB₁，平面BC₁D交AC于D.

(1)求证BD⊥平面ACC₁A₁；

(2)若二面角C₁-BD-C等于60°，求平面BC₁D与平面BCC₁B₁所成二面角的大小.(结果用反三角函数表示)

19.(本小题满分12分)在△ABC中，a、b、c分别为角A、B、C的对边，且，

(1)求角A的度数；

(2)若a=，b+c=3，求b和c的值.

18.(本小题满分12分)已知函数f(x)=log₂(x+m)，且f(0)、f(2)、f(6)成等差数列.

(1)求实数m的值；

(2)若a、b、c是两两不相等的正数，且a、b、c成等比数列，试判断f(a)+f(c)与2f(b)的大小关系，并证明你的结论.

17.(本小题满分12分)甲、乙两名篮球运动员，甲投篮的命中率为0.6，乙投篮的命中率为0.7，两人是否投中相互之间没有影响，求：

(1)两人各投一次，只有一人命中的概率；

(2)每人投篮两次，甲投中1球且乙投中2球的概率.

16.对于任意定义在R上的函数f(x)，若存在x₀∈R满足f(x₀)=x₀，则称x₀是函数

f(x)的一个不动点.若函数f(x)=x²+ax+1没有不动点，则实数a的取值范围是______.

15.已知函数f(x)=2sinωx(ω>0)在［0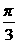，］上单调递增，则ω的取值范围是______.

14.过曲线y=x³－x上点(1，0)的切线方程的一般式是______.