
题目列表(包括答案和解析)
4、若集合 ,
,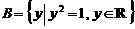 ,则
,则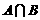 = .
= .
3、将7名学生分配到甲、乙两个宿舍中, 每个宿舍至少安排2名学生, 那么互不相同的分配方案共有_ __ 种.
2、某学校的某一专业从8名优秀毕业生中选派5名支援中国西部开发建设, 其中甲同学必须被选派的概率是_ __.
1、一人口袋里装有大小相同的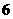 个小球,其中红色、黄色、绿色的球各
个小球,其中红色、黄色、绿色的球各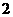 个。如果任意取出
个。如果任意取出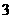 个小球,那么其中恰有
个小球,那么其中恰有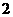 个小球同颜色的概率是 (用分数表示)。
个小球同颜色的概率是 (用分数表示)。
21.解:(Ⅰ)设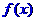 =ax+b(a≠0),则C的方程为:
=ax+b(a≠0),则C的方程为:
y= (x-b),
(x-b),
由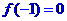 ,得-a+b=0,………………………………… ①
,得-a+b=0,………………………………… ①
由点(2,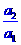 )在曲线C上,得1=
)在曲线C上,得1= (2-b), ………… ②
(2-b), ………… ②
由①、②解得a=b=1,
所以曲线C的方程为y=x-1。
(Ⅱ)由点(n+1,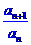 )在曲线C上,有
)在曲线C上,有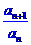 =n,
=n,
于是 =(n-1)!,
=(n-1)!,
即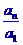 =(n-1)!。a1=1, an=(n-1)!。
=(n-1)!。a1=1, an=(n-1)!。
(Ⅲ)Sn=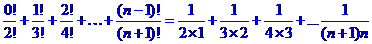
=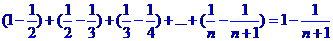 。
。
21. (本题满分10分)设一次函数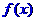 的图象关于直线y=x对称的图象为C,且
的图象关于直线y=x对称的图象为C,且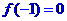 .若点(n+1,
.若点(n+1,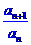 )(n∈N*)在曲线C上,并且a1=a2=1。
)(n∈N*)在曲线C上,并且a1=a2=1。
(Ⅰ)求曲线C的方程;
(Ⅱ)求证: ;
;
(Ⅲ)设Sn= +…+
+…+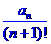 ,求Sn。
,求Sn。
20.解:(I)a2=a1+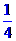 =a+
=a+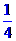 ,a3=
,a3= a2=
a2= a+
a+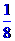 ;
;
(II)因为 a4=a3+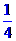 =
= a+
a+ , 所以a5=
, 所以a5= a4=
a4=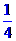 a+
a+ ,
,
所以b1=a1-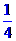 =a-
=a-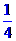 , b2=a3-
, b2=a3-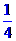 =
= (a-
(a-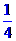 ), b3=a5-
), b3=a5-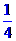 =
=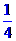 (a-
(a-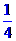 ),
),
猜想:{bn}是公比为 的等比数列。
的等比数列。
证明如下:因为bn+1=a2n+1-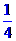 =
= a2n-
a2n-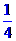 =
= (a2n-1-
(a2n-1-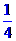 )=
)= bn, (n∈N*)
bn, (n∈N*)
所以{bn}是首项为a-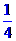 , 公比为
, 公比为 的等比数列·
的等比数列·
(III)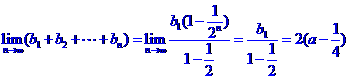 。
。
20.(本题满分10分)设数列{an}的首项a1=a≠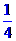 ,且
,且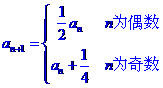 ,
,
记 ,n==l,2,3,…·.
,n==l,2,3,…·.
(I)求a2,a3;
(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)求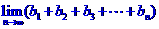 。
。
19. 解:因为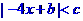 得
得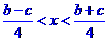
又因为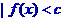 的解集为(-1,2) 所以
的解集为(-1,2) 所以 得b=2。
得b=2。
(Ⅰ)函数 在
在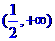 上为增函数。
上为增函数。
证明:设 ,则
,则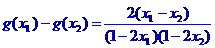
因为 ,所以
,所以
所以 即
即 ,所以,函数
,所以,函数 在
在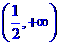 上为增函数。
上为增函数。
(Ⅱ)由 得
得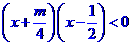 。
。
①当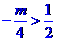 ,即
,即 时,
时,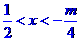 ;②当
;②当 ,即
,即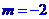 时,无解
时,无解
③当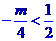 ,即
,即 时,
时,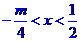
所以,当 时,解集为
时,解集为 ; 当
; 当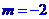 时,解集为空集;
时,解集为空集;
当 时,解集为
时,解集为 。
。
19.(本题满分10分)设函数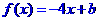 ,不等式
,不等式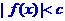 的解集为(-1,2)
的解集为(-1,2)
(Ⅰ)判断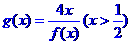 的单调性,并用定义证明;
的单调性,并用定义证明;
(Ⅱ)解不等式 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com