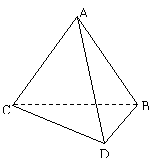
22．(本小题满分14分)如图,异面直线AC与BD的公垂线段AB=4,又AC=2,BD=3,CD=4.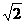

⑴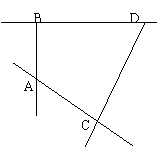求二面角C-AB-D的大小；

⑵求点C到平面ABD的距离；

⑶求异面直线AB与CD间的距离。

21．(本小题满分12分)如图，已知三棱锥S-ABC的三条侧棱长均为10，若且.

　⑴求证：平面SAB⊥平面ABC；

　⑵求：三棱锥S-ABC的体积.

20．(本小题满分12分)梯形BCDQ中，BC∥QD，BC=1，QD=4，过B点的高AB=1，且A点平分QD，将△QBA沿AB折起，记折起后点Q的位置为P，且使平面PAB⊥平面ABCD

⑴求证：平面PCD⊥平面PAC；

⑵求直线AD与平面PCD所成角的正弦值；

⑶求二面角A-PD-C的正弦值.

18．(本小题满分12分)正三棱柱ABC-A₁B₁C₁的侧棱长和底面边长都等于2，D是BC上一点，且AD⊥BC.

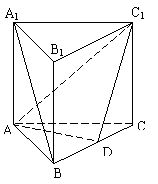⑴求证：A₁B∥平面ADC₁;

⑵求截面ADC₁与侧面ACC₁A₁所成的二面角D-AC₁-C的大小.

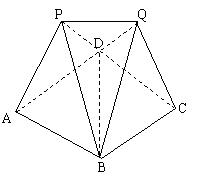　　　　　 　　　　　　　　　　　　　　　　　　　 19．(本小题满分12分)如图，某建筑物的基本单元可近似地按以下方法构作：先在地平面内作菱形ABCD，其边长为1，∠BAD＝60°，再在平面的上侧，分别以△ABD与△CBD为底面安装上相同的正三棱锥P－ABD与Q－CBD，∠APB＝90°。

⑴求证：PQ⊥BD；

⑵求二面角P－BD－Q的大小；

⑶求点P到平面QBD的距离。

17．(本小题满分12分)如图，将一副三角板拼接，使它们有公共边BC，且使两个三角形所在的平面互相垂直，若∠BAC＝90°，AB＝AC，∠CBD＝90°，∠BDC＝60°，BC＝6。

⑴求证：平面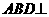平面ACD；

⑵求二面角的平面角的正切值；

⑶设过直线AD且与BC平行的平面为，求点B到平面的距离。

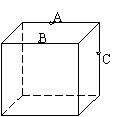
16．右图为一正方体，A、B、C分别为所在边的中点，过A、B、C三点

的平面与此正方体表面相截，则其截痕的形状是　　　　 .

15．将直角三角形ABC沿斜边上的高AD折成120°的二面角，已知直角边

，那么二面角A-BC-D的正切值为　　　　　 .

14．将正方形ABCD沿着对角线BD折成一个四面体ABCD，在下列给出的四个角度中，

①30° ②60° ③90° ④120°，不可能是AC与平面BCD所成的角是　　　　 ．(把你认为正确的序号都填上)

13．有三个球和一个正方体，第一个球与正方体各个面相内切，第二球与正方体各条棱相切，第三个球过正方体各顶点，则这三个球的面积之比为________。

12．已知a－l－b是大小确定的一个二面角，若a,b是空间两条直线，则能使a,b所成的角为定值的一个条件是　　　　　　 　　　　　　　　　　　　　　　　 (　　 )

　　　 A．a⊥a且b⊥b　　　 B．a∥a且b⊥b　　　 C．a⊥a且b∥b　　　 D．a∥a且b∥b