
题目列表(包括答案和解析)
2.(福建)直线x+2y=0被曲线x2+y2-6x-2y-15=0所截得的弦长等于 .
⒈直线和圆的方程 (1)理解直线的倾斜角和斜率的概念,掌握过两点的直线的斜率公式.掌握直线方 程的点斜式、两点式、一般式,并能根据条件熟练地求出直线方程. (2)掌握两条直线平行与垂直的条件,两条直线所成的角和点到直线的距离公式.能够根据直线的方程判断两条直线的位置关系. (3)了解二元一次不等式表示平面区域. (4)了解线性规划的意义,并会简单的应用. (5)了解解析几何的基本思想,了解坐标法. (6)掌握圆的标准方程和一般方程,了解参数方程的概念,理解圆的参数方程. ⒉圆锥曲线方程 (1)掌握椭圆的定义、标准方程和椭圆的简单几何性质,理解椭圆的参数方程. (2)掌握双曲线的定义、标准方程和双曲线的简单几何性质. (3)掌握抛物线的定义、标准方程和抛物线的简单几何性质. (4)了解圆锥曲线的初步应用. 二、高考试题回放
1.(福建)已知F1、F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A、B两点,若△ABF2是正三角形,则这个椭圆的离心率是 ( )
A. B.
B.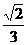 C.
C. D.
D.
2.垂直转化

每一垂直或平行的判定就是从某一垂直或平行开始转向另一垂直或平行最终达到目的.
例如:有两个平面垂直时,一般要用性质定理,在一个平面内作交线的垂线,使之转化为线面垂直,然后进一步转化为线线垂直.
1.平行转化

3设X、Y、Z是空间不同的直线或平面,对下面四种情形,使“X⊥Z且Y⊥Z X∥Y”为真命题的是_________(填序号).
X∥Y”为真命题的是_________(填序号).
①X、Y、Z是直线 ②X、Y是直线,Z是平面 ③Z是直线,X、Y是平面 ④X、Y、Z是平面
、3.解析:①是假命题,直线X、Y、Z位于正方体的三条共点棱时为反例,②③是真命题,④是假命题,平面X、Y、Z位于正方体的三个共点侧面时为反例.
答案:②③
4.设a,b是异面直线,下列命题正确的是__.④_______.
①过不在a、b上的一点P一定可以作一条直线和a、b都相交
②过不在a、b上的一点P一定可以作一个平面和a、b都垂直
③过a一定可以作一个平面与b垂直
④过a一定可以作一个平面与b平行
例二:两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证:MN∥平面BCE.
命题意图:本题主要考查线面平行的判定,面面平行的判定与性质,以及一些平面几何的知识。
知识依托:解决本题的关键在于找出面内的一条直线和该平面外的一条直线平行,即线(内)∥线(外) 线(外)∥面.或转化为证两个平面平行.
线(外)∥面.或转化为证两个平面平行.
技巧与方法:证法一利用线面平行的判定来证明.证法二采用转化思想,通过证面面平行来证线面平行.
证法一:作MP⊥BC,NQ⊥BE,P、Q为垂足,则MP∥AB,NQ∥AB.
∴MP∥NQ,又AM=NF,AC=BF,
∴MC=NB,∠MCP=∠NBQ=45°
∴Rt△MCP≌Rt△NBQ
∴MP=NQ,故四边形MPQN为平行四边形
∴MN∥PQ
∵PQ 平面BCE,MN在平面BCE外,
平面BCE,MN在平面BCE外,
∴MN∥平面BCE.

证法二:如图过M作MH⊥AB于H,则MH∥BC,
∴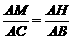
连结NH,由BF=AC,FN=AM,得

∴MN∥平面BCE.
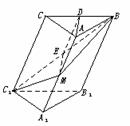 [例2]在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
[例2]在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
(1)若D是BC的中点,求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;
(3)AM=MA1是截面MBC1⊥平面BB1C1C的充要条件吗?请你叙述判断理由.
命题意图:本题主要考查线面垂直、面面垂直的判定与性质,
知识依托:线面垂直、面面垂直的判定与性质.
技巧与方法:本题属于知识组合题类,关键在于对题目中条件的思考与分析,掌握做此类题目的一般技巧与方法,以及如何巧妙作辅助线.
(1)证明:∵AB=AC,D是BC的中点,∴AD⊥BC
∵底面ABC⊥平面BB1C1C,∴AD⊥侧面BB1C1C
∴AD⊥CC1.
(2)证明:延长B1A1与BM交于N,连结C1N
∵AM=MA1,∴NA1=A1B1
∵A1B1=A1C1,∴A1C1=A1N=A1B1
∴C1N⊥C1B1
∵底面NB1C1⊥侧面BB1C1C,∴C1N⊥侧面BB1C1C
∴截面C1NB⊥侧面BB1C1C
∴截面MBC1⊥侧面BB1C1C.
(3)解:结论是肯定的,充分性已由(2)证明,下面证必要性.
过M作ME⊥BC1于E,∵截面MBC1⊥侧面BB1C1C
∴ME⊥侧面BB1C1C,又∵AD⊥侧面BB1C1C.
∴ME∥AD,∴M、E、D、A共面
∵AM∥侧面BB1C1C,∴AM∥DE
∵CC1⊥AM,∴DE∥CC1
∵D是BC的中点,∴E是BC1的中点
∴AM=DE= AA1,∴AM=MA1.
AA1,∴AM=MA1.
课堂小结:垂直和平行涉及题目的解决方法须熟练掌握两类相互转化关系:
2. 解析:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,在a′上任取一点A,过A作AC⊥l,垂足为C,则AC⊥β,过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,∴△APB为直角三角形,故∠APB为锐角.
解析:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,在a′上任取一点A,过A作AC⊥l,垂足为C,则AC⊥β,过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,∴△APB为直角三角形,故∠APB为锐角.
答案:C
2.在直二面角α-l-β中,直线a α,直线b
α,直线b β,a、b与l斜交,则( )
β,a、b与l斜交,则( )
A.a不和b垂直,但可能a∥b B.a可能和b垂直,也可能a∥b
C.a不和b垂直,a也不和b平行 D.a不和b平行,但可能a⊥b
1.在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是( )
A. B.
B.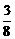 C.
C. D.
D.
解析:如图,设A1C1∩B1D1=O1,∵B1D1⊥A1O1,B1D1⊥AA1,∴B1D1⊥平面AA1O1,故平面AA1O1⊥AB1D1,交线为AO1,在面AA1O1内过A1作A1H⊥AO1于H,则易知A1H长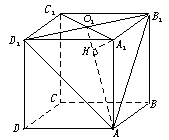 即是点A1到平面AB1D1的距离,在Rt△A1O1A中,A1O1=
即是点A1到平面AB1D1的距离,在Rt△A1O1A中,A1O1=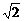 ,AO1=3
,AO1=3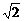 ,由A1O1·A1A=h·AO1,可得A1H=
,由A1O1·A1A=h·AO1,可得A1H= .
.
答案:C
6、规范书写、应对网上阅卷
今年网上阅卷的选择题、填空题、解答题书写在一份答卷纸上,与以往高考的答题模式不一样。为了便于网上阅卷,要求考生在做图和书写时,要用50毫米的黑色签字笔,希望考生要强化适应训练。因为,高考的得分是以学生的书写为依据,书写规范不规范,会不会书写直接影响高考的评分。 五附三课时教案
垂直与平行
垂直与平行是高考的重点内容之一,考查内容灵活多样.本节主要帮助考生深刻理解线面平行与垂直、面面平行与垂直的判定与性质,并能利用它们解决一些问题.
例一:选择题与填空题
5、二轮复习,我们也要注意关注、搜集、分析学生一轮复习的学情,针对出现的问题做到有的放矢的复习并进行强化训练。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com