2.3、能力立意，渗透数学思想：如河南第(21)题，将双曲线的方程、性质与坐标法、定比分点的坐标公式、向量、离心率等知识融为一体，有很强的综合性。

2.2　 整体平衡，重点突出：《考试大纲》中解析几何部分有27个知识点，一般考查16 至18 个，其中对直线、线性归划、圆、圆锥曲线等知识的考查几乎没有遗漏，通过对知识的重新组合，考查时既注意全面，更注意突出重点， 对支撑数学科知识体系的主干知识， 考查时保证较高的比例并保持必要深度。

2.1　 题型稳定：近几年来高考解析几何试题一直稳定在1~2个选择题，1个填空题，1个解答题上，分值约为30分， 占总分值的20%左右。

2、高考试题的特点：

1、知识点列表综述

试卷名称	福建	湖北	湖南	广东	江苏
知识点提要	直线与椭圆，椭圆的离心率，直线与圆，直线与抛物线，轨迹方程，变量范围，导数与抛物线结合。	直线方程，线段定比分点坐标，两圆的位置关系，直线与双曲线，双曲线与圆。	双曲线几何性质，椭圆性质，直线与抛物线，线段定比分点，抛物线与圆和向量、导数结合。	双曲线的几何性质，直线与圆，直线与椭圆、双曲线及线段定比分点结合。	双曲线与抛物线的准线，双曲线的离心率，直线与圆相切，线性规划，椭圆方程，直线直线与椭圆，直线的斜率。
试卷名称 　 　 　 知识点提要	辽宁 　 双曲线定义，直线与圆相切，直线截距，直线与椭圆，与向量结合，轨迹方程，最大值与最小值。	上海 　 抛物线方程，准线方程，直线和圆，圆的方程，直线与抛物线，对称，最大值。	重庆 　 直线与圆，双曲线准线，离心率，最大值，直线与圆、抛物线结合、面积最大值。	河南 　 直线与椭圆、焦点、距离，直线与抛物线的准线、直线斜率的范围，直线与圆、轨迹方程，直线与双曲线、离心率范围、与向量结合。	四川 　 点到直线距离，直线方程，椭圆与双曲线方程、离心率，直线与抛物线、向量、直线截距范围结合。

37．(宁夏)双曲线的焦点距为2c，直线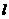过点(a，0)和(0，b)，且点(1，0)到直线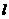的距离与点(－1，0)到直线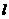的距离之和求双曲线的离心率e的取值范围.

36．(宁夏)设满足约束条件：

则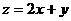的最大值是　　　　　　　　 .

35．(宁夏)已知椭圆的中心在原点，离心率，且它的一个焦点与抛物线的焦点重合， 则此椭圆方程为　　 　　　　　　　　　　　　　　　　　　　 (　　 )

A．　　 B．　　 C．　　　　　　 D．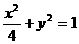

34．(宁夏)过点(－1，3)且垂直于直线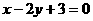的直线方程为　　　　　 (　　 )

　　　 A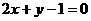．　　　　　　　　　　　　　　　　　 B．

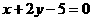　　　 C．　　　　　　　　　　　　　　　　　 D．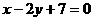

33、(四川)给定抛物线C：y²=4x，F是C的焦点，过点F的直线l与C相交于A、B两点。 (Ⅰ)设l的斜率为1，求与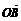的夹角的大小；

(Ⅱ)设，若λ∈[4,9]，求l在y轴上截距的变化范围.