
题目列表(包括答案和解析)
3、注意解析几何与相关学科的交叉问题 由于解析几何内容在直线与圆锥曲线的几何性质和综合应用方面,涉及的内容丰富,易于纵横联系,对培养学生的数学素质,提高能力和继续学习有重要作用。这就启示我们在备考复习中,应高度重视解析几何与相关学科交叉知识问题的综合应用。04年高考题也给我们揭示了重视这一问题的重要性。应该说,解析几何中的圆锥曲线都是与方程理论相联系的,但在复习过程中,我们不应只停留在这一联系,而应尽可能加强解析几何和函数,解析几何与导数、平面向量的联系。在此,我们特别强调的是应有机加大解几和函数有关性质的联系。
2.3复习中要掌握常用的解题策略
平面解析几何是综合性较强的学科,因而解题时就需要运用多种知识、采用多种数学手段。熟记各种定义、基本公式、法则,做到迅速、准确解题。
2.2要强化解析几何的基本思想和方法
解析几何的基本思想是在平面直角坐标系中,把点与实数对,曲线与方程,区域与不等式统一起来,用代数方法研究平面上的几何问题.其中最重点的内容是用方程研究曲线,其次是用不等式研究区域问题.研究这一基本思想的实质是等价转化的思想。
2.1要掌握求曲线方程的思路和方法.
求曲线方程的方法有多种,但其思路的实质都是根据曲线上点适合的共同条件找出动点的流动坐标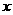 和
和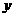 之间的关系式。常见的求曲线方程的类型有两种,一种是曲线形状明确且便于用标准形式表示,这时可用特定系数法求其方程;一种是曲线形状不明确或不便于用标准形式表示,这时一般地可用直接法,间接代点法,参数法等求方程。
之间的关系式。常见的求曲线方程的类型有两种,一种是曲线形状明确且便于用标准形式表示,这时可用特定系数法求其方程;一种是曲线形状不明确或不便于用标准形式表示,这时一般地可用直接法,间接代点法,参数法等求方程。
2、突出“曲线与方程”这一重点内容.
解析几何有两个主要问题,一是由曲线求方程;二是由方程研究曲线,复习时选题要突出这两个问题.
1、重视教材的基础作用和示范作用
高考试题年年变,但命题的依据是《考试大纲》,要以此为根本,弄清高考的知识点及对基础知识与能力的要求,这中间实质性的工作就是精通课本,客观题一般直接来源于课本,往往是课本的原题或变式题,解析几何的主观试题的生长点也是课本,所以在复习中要精通课本,贯彻“源于课本,高于课本”的原则.在二轮复习选题时,客观题可以根据课本题改变,加强知识点的覆盖,同时还要注意知识的综合。
高考解析几何的命题一般紧扣课本, 突出重点, 全面考查. 选择题和填空题考查直线, 圆, 圆锥曲线中的基础知识. 解答题重点考查圆锥曲线中的重要知识点, 通过知识的重组与链接, 使知识形成网络, 着重考查直线与圆锥曲线的位置关系, 求解有时还要用到平几的基本知识。
解析几何解答题在历年的高考中常考常新, 体现在重视能力立意, 强调思维空间, 是用活题考死知识的典范. 考题求解时考查了等价转化, 数形结合, 分类讨论, 函数与方程等数学思想, 以及定义法, 配方法, 待定系数法, 参数法, 判别式法等数学通法.
例1 已知点T是半圆O的直径AB上一点,AB=2、OT=t (0<t<1),以AB为直腰作直角梯形 ,使
,使 垂直且等于AT,使
垂直且等于AT,使 垂直且等于BT,
垂直且等于BT, 交半圆于P、Q两点,建立如图所示的直角坐标系.
交半圆于P、Q两点,建立如图所示的直角坐标系.
(1)写出直线 的方程;
的方程;
(2)计算出点P、Q的坐标;
(3)证明:由点P发出的光线,经AB反射后,反射光线通过点Q.
解: 通过读图, 看出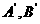 点的坐标.
点的坐标.
 (1 ) 显然
(1 ) 显然 ,
,  于是 直线
于是 直线
的方程为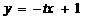 ;
;
(2)由方程组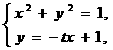
解出 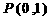 、
、 ;
;
(3) ,
,
 .
.
由直线PT的斜率和直线QT的斜率互为相反数知,由点P发出的光线经点T反射,反射光线通过点Q.
需要注意的是, Q点的坐标本质上是三角中的万能公式, 有趣吗?
例2 已知直线l与椭圆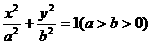 有且仅有一个交点Q,且与x轴、y轴分别交于R、S,求以线段SR为对角线的矩形ORPS的一个顶点P的轨迹方程.
有且仅有一个交点Q,且与x轴、y轴分别交于R、S,求以线段SR为对角线的矩形ORPS的一个顶点P的轨迹方程.
解:从直线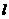 所处的位置, 设出直线
所处的位置, 设出直线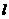 的方程,
的方程,
由已知,直线l不过椭圆的四个顶点,所以设直线l的方程为
代入椭圆方程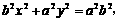 得
得
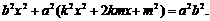
化简后,得关于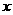 的一元二次方程
的一元二次方程
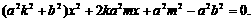
于是其判别式
由已知,得△=0.即 ①
①
在直线方程 中,分别令y=0,x=0,求得
中,分别令y=0,x=0,求得
令顶点P的坐标为(x,y), 由已知,得
代入①式并整理,得
 , 即为所求顶点P的轨迹方程.
, 即为所求顶点P的轨迹方程.
方程 形似椭圆的标准方程, 你能画出它的图形吗?
形似椭圆的标准方程, 你能画出它的图形吗?
例3已知双曲线 的离心率
的离心率 ,过
,过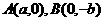 的直线到原点的距离是
的直线到原点的距离是 (1)求双曲线的方程;(2)已知直线
(1)求双曲线的方程;(2)已知直线 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
解:∵(1) 原点到直线AB:
原点到直线AB: 的距离
的距离 .
.
故所求双曲线方程为 
(2)把 中消去y,整理得
中消去y,整理得  .
.
设 的中点是
的中点是 ,则
,则
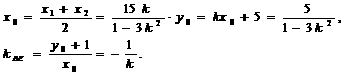

即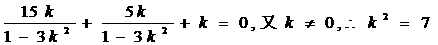
故所求k=± .
.
为了求出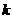 的值, 需要通过消元, 想法设法建构
的值, 需要通过消元, 想法设法建构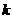 的方程.
的方程.
例4 已知椭圆C的中心在原点,焦点F1、F2在x轴上,点P为椭圆上的一个动点,且∠F1PF2的最大值为90°,直线l过左焦点F1与椭圆交于A、B两点,△ABF2的面积最大值为12.
(1)求椭圆C的离心率;
(2)求椭圆C的方程.
解:(1)设 , 对
, 对 由余弦定理, 得
由余弦定理, 得
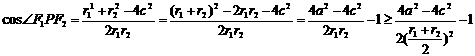
 ,解出
,解出 
(2)考虑直线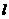 的斜率的存在性,可分两种情况:
的斜率的存在性,可分两种情况:
i) 当k存在时,设l的方程为 ………………①
………………①
椭圆方程为
由 得
得  .
.
于是椭圆方程可转化为  ………………②
………………②
将①代入②,消去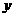 得
得 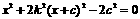 ,
,
整理为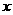 的一元二次方程,得
的一元二次方程,得
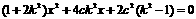 .
.
则x1、x2是上述方程的两根.且
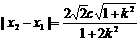 ,
,
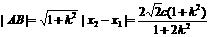 ,
,
|
 AB边上的高
AB边上的高
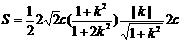

ii) 当k不存在时,把直线 代入椭圆方程得
代入椭圆方程得


由①②知S的最大值为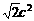 由题意得
由题意得 =12 所以
=12 所以

故当△ABF2面积最大时椭圆的方程为: 
下面给出本题的另一解法,请读者比较二者的优劣:
设过左焦点的直线方程为: …………①
…………①
(这样设直线方程的好处是什么?还请读者进一步反思反思.)
椭圆的方程为:
由 得:
得: 于是椭圆方程可化为:
于是椭圆方程可化为: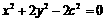 ……②
……②
把①代入②并整理得:
于是 是上述方程的两根.
是上述方程的两根.


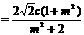 ,
,
AB边上的高 ,
,
从而

当且仅当m=0取等号,即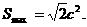
由题意知 , 于是
, 于是  .
.
故当△ABF2面积最大时椭圆的方程为: 
例5 已知直线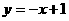 与椭圆
与椭圆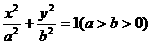 相交于A、B两点,且线段AB的中点在直线
相交于A、B两点,且线段AB的中点在直线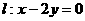 上.
上.
(1)求此椭圆的离心率;
(2 )若椭圆的右焦点关于直线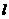 的对称点的在圆
的对称点的在圆 上,求此椭圆的方程.
上,求此椭圆的方程.
解:(1)设A、B两点的坐标分别为 得
得

 ,
,
根据韦达定理,得

∴线段AB的中点坐标为( ).
).
由已知得
故椭圆的离心率为 .
.
(2)由(1)知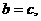 从而椭圆的右焦点坐标为
从而椭圆的右焦点坐标为 设
设 关于直线
关于直线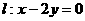 的对称点为
的对称点为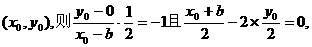
解得 
由已知得 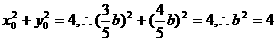
故所求的椭圆方程为 .
.
例6 已知⊙M: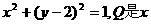 轴上的动点,QA,QB分别切⊙M于A,B两点,
轴上的动点,QA,QB分别切⊙M于A,B两点,
(1)如果 ,求直线MQ的方程;
,求直线MQ的方程;
(2)求动弦AB的中点P的轨迹方程.
解:(1)由 ,可得
,可得 由射影定理,得
由射影定理,得 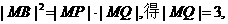 在Rt△MOQ中,
在Rt△MOQ中,

 ,
,
故 ,
,
所以直线AB方程是

(2)连接MB,MQ,设 由
由
点M,P,Q在一直线上,得
 由射影定理得
由射影定理得
即 把(*)及(**)消去a,并注意到
把(*)及(**)消去a,并注意到 ,可得
,可得
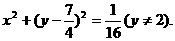
适时应用平面几何知识,这是快速解答本题的要害所在,还请读者反思其中的奥妙.
例7
如图,在Rt△ABC中,∠CBA=90°,AB=2,AC= 。DO⊥AB于O点,OA=OB,DO=2,曲线E过C点,动点P在E上运动,且保持| PA |+| PB |的值不变.
。DO⊥AB于O点,OA=OB,DO=2,曲线E过C点,动点P在E上运动,且保持| PA |+| PB |的值不变.
(1)建立适当的坐标系,求曲线E的方程;
(2)过D点的直线L与曲线E相交于不同的两点M、N且M在D、N之间,设 ,
,
试确定实数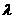 的取值范围.
的取值范围.
解: (1)建立平面直角坐标系, 如图所示 .
 ∵| PA |+| PB |=| CA |+| CB |
∵| PA |+| PB |=| CA |+| CB |
=
∴动点P的轨迹是椭圆
∵
∴曲线E的方程是  .
.
(2)设直线L的方程为  , 代入曲线E的方程
, 代入曲线E的方程 ,得
,得
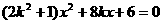
设M1( , 则
, 则
|

i)
L与y轴重合时,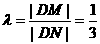
ii) L与y轴不重合时,
由①得 
又∵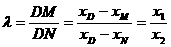 ,
,
∵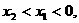 或
或 
∴0<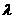 <1 ,
<1 ,
∴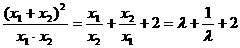 .
.
∵
而 ∴
∴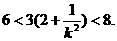
∴ 
∴  ,
,  ,
,
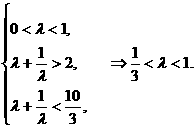 ∴
∴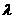 的取值范围是
的取值范围是 .
.
值得读者注意的是,直线L与y轴重合的情况易于遗漏,应当引起警惕.
例8
直线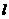 过抛物线
过抛物线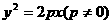 的焦点,且与抛物线相交于A
的焦点,且与抛物线相交于A 两点.
两点.
(1)求证: ;
;
(2)求证:对于抛物线的任意给定的一条弦CD,直线l不是CD的垂直平分线.
解: (1)易求得抛物线的焦点. 
若l⊥x轴,则l的方程为 .
.
若l不垂直于x轴,可设 ,代入抛物线方程整理得
,代入抛物线方程整理得  .
.
综上可知  .
.
(2)设 ,则CD的垂直平分线
,则CD的垂直平分线 的方程为
的方程为
假设 过F,则
过F,则 整理得
整理得


 ,
,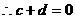 .
.
这时 的方程为y=0,从而
的方程为y=0,从而 与抛物线
与抛物线 只相交于原点. 而l与抛物线有两个不同的交点,因此
只相交于原点. 而l与抛物线有两个不同的交点,因此 与l不重合,l不是CD的垂直平分线.
与l不重合,l不是CD的垂直平分线.
此题是课本题的深化,你能够找到它的原形吗?知识在记忆中积累,能力在联想中提升. 课本是高考试题的生长点,复习忌忘掉课本!
3、综合试题的热点问题:
热点之一:圆锥曲线的定义、圆锥曲线方程 圆锥曲线定义是其一切几何性质的“根”与“源”,是建立曲线方程的基础,揭示了圆锥曲线上的点与焦点及准线间的关系,是解几综合题的重要背景。圆锥曲线的方程是研究几何性质的重要载体。
热点之二:函数与方程的思想 函数与方程的思想是贯穿于解析几何的一条主线,很多解几综合题往往都是以最值问题或圆锥曲线的基本量的求解为依托,通过转化,运用函数与方程的思想加以解决。
热点之三:与圆锥曲线有关的轨迹问题 解析几何的核心就是用方程的思想研究曲线,用曲线的性质研究方程。轨迹问题正是体现这一思想的重要形式。运用定义法、代入法、参数法、结合问题的几何特征,可以较好的求解。
热点之四:曲线组合 除了直线和圆锥曲线是传统的结合外,04年的高考题大量出现了圆与双曲线、圆与抛物线、双曲线与抛物线等的结合。
热点之五:与平面向量、导数等新增内容相结合 利用一切可以利用的机会有机结合。
热点之六:最值及离心率范围问题 通过求最值及离心率的范围问题达到与函数、方程、不等式等主干知识链接。
2.5、难度下降, 位置不定:近几年解析几何试题的难度有所下降, 选择题、填空题均属易中等题,且解答题不再处于压轴题的位置,计算量减少,思考量增大。
2.4、与新教材融合,注意知识的链接:与导数的几何意义、平面向量相结合,与导数结合仅仅停留在对称轴平行于y轴的抛物线上,能与向量结合的试题几乎都联系上。解析几何与函数、方程、不等式等主干知识的结合,几乎各省的解答题都有联系。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com