
题目列表(包括答案和解析)
18.(浙江卷)袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,共摸5次.(i)恰好有3次摸到红球的概率;(ii)第一次、第三次、第五次摸到红球的概率.
(Ⅱ) 若A、B两个袋子中的球数之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是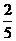 ,求p的值.
,求p的值.
解: (I)(i) 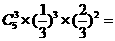


(ii) =
=
(II)设袋子A中有 个球,则袋子B中有2
个球,则袋子B中有2 个球
个球
由 得
得
17.(辽宁卷)
 某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级.对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品.
某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级.对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品.
(Ⅰ)已知甲、乙两种产品每一道工序的加工结果为A级的概率如表一所示,分别求生产出的甲、乙产品为一等品的概率P甲、P乙;
(Ⅱ)已知一件产品的利润如表二所示,用ξ、η分别表示一件甲、乙产品的利润,在(I)的条件下,求ξ、η的分布列及Eξ、Eη;
(Ⅲ)已知生产一件产品需用的工人数和资金额如表三所示.该工厂有工人40名,可用资金60万元.设x、y分别表示生产甲、乙产品的数量,在(II)的条件下,x、y为何值时,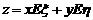 最大?最大值是多少? (解答时须给出图示)
最大?最大值是多少? (解答时须给出图示)
(Ⅰ)解: …………2分
…………2分
 (Ⅱ)解:随机变量
(Ⅱ)解:随机变量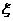 、
、 的分别列是
的分别列是

 …………6分
…………6分
 (Ⅲ)解:由题设知
(Ⅲ)解:由题设知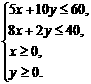 目标函数为
目标函数为  ……8分
……8分
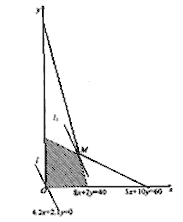
作出可行域(如图):
作直线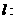

将l向右上方平移至l1位置时,直线经过可行域上
的点M点与原点距离最大,此时 …………10分
…………10分
取最大值. 解方程组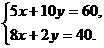
得 即
即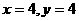 时,z取最大值,z的最大值为25.2 .……………12分
时,z取最大值,z的最大值为25.2 .……………12分
16.(江西卷)A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝上时A赢得B一张卡片,否则B赢得A一张卡片,如果某人已赢得所有卡片,则游戏终止.求掷硬币的次数不大于7次时游戏终止的概率.
解:(1)设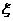 表示游戏终止时掷硬币的次数,
表示游戏终止时掷硬币的次数,
设正面出现的次数为m,反面出现的次数为n,则 ,可得:
,可得:


15.(江西卷)A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝上时A赢得B一张卡片,否则B赢得A一张卡片.规定掷硬币的次数达9次时,或在此前某人已赢得所有卡片时游戏终止.设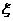 表示游戏终止时掷硬币的次数.
表示游戏终止时掷硬币的次数.
(1)求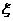 的取值范围;
的取值范围;
(2)求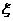 的数学期望E
的数学期望E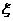 .
.
解:(1)设正面出现的次数为m,反面出现的次数为n,则 ,可得:
,可得:

(2)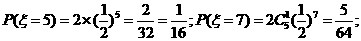

20、(1)设“甲射击4次,至少1次未击中目标”为事件A,则其对立事件 为“4次均击中目标”,则
为“4次均击中目标”,则
(2)设“甲恰好击中目标2次且乙恰好击中目标3次”为事件B,则

(3)设“乙恰好射击5次后,被中止射击”为事件C,由于乙恰好射击5次后被中止射击,故必然是最后两次未击中目标,第三次击中目标,第一次及第二次至多有一次未击中目标。
故
14.(江苏卷)甲、乙两人各射击一次,击中目标的概率分别是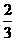 和
和 .假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
(Ⅰ)求甲射击4次,至少1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?
13.(湖南卷)某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
(Ⅰ)求ξ的分布及数学期望;
(Ⅱ)记“函数f(x)=x2-3ξx+1在区间[2,+∞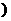 上单调递增”为事件A,求事件A的概率.
上单调递增”为事件A,求事件A的概率.
解:(I)分别记“客人游览甲景点”,“客人游览乙景点”,“客人游览丙景点”
为事件A1,A2,A3. 由已知A1,A2,A3相互独立,P(A1)=0.4,P(A2)=0.5,
P(A3)=0.6.
客人游览的景点数的可能取值为0,1,2,3. 相应地,客人没有游览的景点数的可能取
值为3,2,1,0,所以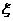 的可能取值为1,3.
的可能取值为1,3.
P(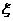 =3)=P(A1·A2·A3)+ P(
=3)=P(A1·A2·A3)+ P( )
)
= P(A1)P(A2)P(A3)+P( )
)
=2×0.4×0.5×0.6=0.24,
|
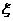 =1)=1-0.24=0.76.
=1)=1-0.24=0.76.
所以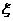 的分布列为
的分布列为
E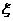 =1×0.76+3×0.24=1.48.
=1×0.76+3×0.24=1.48.
(Ⅱ)解法一 因为
所以函数 上单调递增,
上单调递增,
要使 上单调递增,当且仅当
上单调递增,当且仅当
从而
解法二: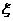 的可能取值为1,3.
的可能取值为1,3.
当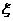 =1时,函数
=1时,函数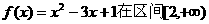 上单调递增,
上单调递增,
当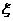 =3时,函数
=3时,函数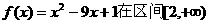 上不单调递增.0
上不单调递增.0
所以
2.只有当事件A,B互斥时,才能运用公式P(A+B)=P(A)+P(B);只有当事件A,B相互独立时,才能运用公式P(A·B)=P(A)·P(B).
20.分析:设抽到合格产品的事件分别为A,B,C,则
P(A)=0.90 P(B)=P(C)=0.95
P( )=0.10
P(
)=0.10
P(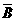 )=P(
)=P(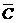 )=0.05
)=0.05
(Ⅰ)因为A,B,C相互独立,故恰有一件不合格的概率为:
P(A·B·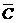 )+_P(A·
)+_P(A·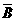 ·C)+P(
·C)+P( ·B·C)
·B·C)
=P(A)·P(B)·P(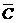 )+P(A)·P(
)+P(A)·P(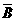 )·P(C)+P(
)·P(C)+P( )·P(B)·P(C)
)·P(B)·P(C)
=0.90×0.95×0.05+0.90×0.05×0.95+0.10×0.95×o.95
=0.176
(Ⅱ)至少有两件不合格的概率为:
P(A·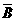 ·
·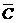 )+P(
)+P( ·B·
·B·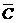 )+P(
)+P( ·
·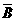 ·C)+P(
·C)+P( ·
·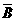 ·
·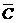 )
)
=0.90×0.05×0.05+0.10×0.95×0.05+0.10×0.05×0.95+0.10×0.05×0.05
=0.012
思路:1.正确分清互斥事件与相互独立事件是解决此类问题的关键.
16. ; 17.0.05 ; 18.
; 17.0.05 ; 18. ;19. ①③
;19. ①③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com